
科目:初中数学 来源:山东省济南历下区2018届一模数学试卷 题型:解答题
如图,已知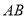 是
是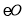 的直径,CD与
的直径,CD与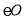 相切于C,
相切于C, 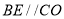 .
.
(1)求证:BC 是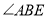 的平分线.
的平分线.
(2)若DC=8, 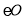 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
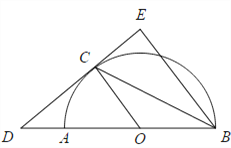
【答案】(1)证明见解析;(2)4.8
【解析】分析:(1)由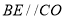 ,推出
,推出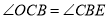 ,由
,由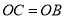 ,推出
,推出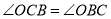 ,可得
,可得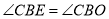 .(2)在
.(2)在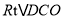 中,求出OD,由
中,求出OD,由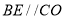 ,可得
,可得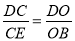 ,由此即可解决问题.
,由此即可解决问题.
详【解析】
(1)证明:因为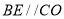 ,
,
所以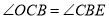 ,
,
又因为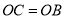 ,
,
所以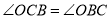 ,
,
故可得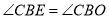 ,
,
即可得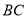 是
是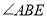 的平分线.
的平分线.
(2)因为DE是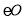 的切线,
的切线,
所以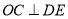 ,即在
,即在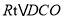 中,DC=8,OC=OA=6,所以
中,DC=8,OC=OA=6,所以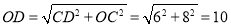 ,
,
又因为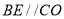 ,
,
所以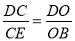 ,
,
所以 ,
,
即可得EC=4.8
点睛:本题主要考查了切线的性质及相似三角形的应用,题目难度适中,会综合运用所考查的知识点是解题的关键.
【题型】解答题
【结束】
23
“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
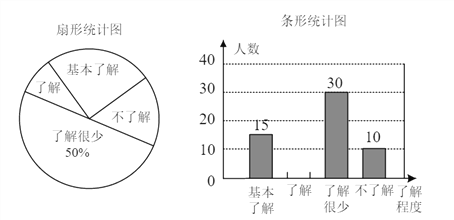
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____ .
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源:北京市2018届初三数学中考复习 综合练习题 含答案 题型:解答题
如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE= ∠A.
∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB= ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).

查看答案和解析>>
科目:初中数学 来源:北京市2018届初三数学中考复习 综合练习题 含答案 题型:填空题
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:(1)EF= OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF= OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;(5)OG·BD=AE2+CF2,其中正确的是__.
;(5)OG·BD=AE2+CF2,其中正确的是__.

查看答案和解析>>
科目:初中数学 来源:北京市2018届初三数学中考复习 综合练习题 含答案 题型:单选题
下列运算正确的是( )
A. ﹣a•a3=a3 B. ﹣(a2)2=a4 C. x﹣ x=
x= D. (
D. (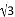 ﹣2)(
﹣2)(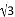 +2)=﹣1
+2)=﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com