
若M= ,N
,N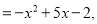 则2M-N的结果是( )
则2M-N的结果是( )
A. 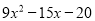 B.
B. 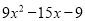 C.
C. 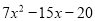 D.
D. 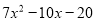
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源:安徽省芜湖市2017-2018学年度第一学期期末考试八年级数学试卷 题型:单选题
化简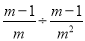 的结果是( )
的结果是( )
A. 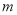 B.
B. 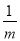 C.
C. 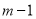 D.
D. 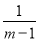
查看答案和解析>>
科目:初中数学 来源:安徽省豪州市心校2017-2018学年度第一学期期末八年级数学试卷 题型:填空题
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为 .
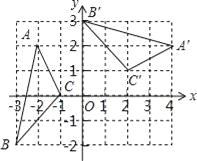
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
已知:点P是直线MN外一点,点A、B、C是直线MN上三点,分别连接PA、PB、PC.
(1)通过测量的方法,比较PA、PB、PC的大小,直接用“>”连接;
(2)在直线MN上能否找到一点D,使PD的长度最短?如果有,请在图中作出线段PD,并说明它的理论依据;如果没有,请说明理由.
见解析 【解析】试题分析:(1)通过测量不难得出PA>PB>PC;由于点到直线的距离垂线段最短,所以过点P作PD⊥MN交MN于点D. 试题解析: 【解析】 (1)通过测量可知,PA>PB>PC; (2)过点P作PD⊥MN,则PD最短. (垂线段最短).查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
比大小:-2_____-3.
> 【解析】数轴上,-2位于-3的右侧,所以-2>-3. 故答案为>.查看答案和解析>>
科目:初中数学 来源:四川省遂宁市蓬溪县2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
如果a+b<0,并且ab>0,那么( ).
A. a>0,b>0 B. a<0,b<0 C. a<0,b>0 D. a>0,b<0
B 【解析】由ab>0可得:a、b同号; 由a+b<0可得:a<0,b<0. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型:解答题
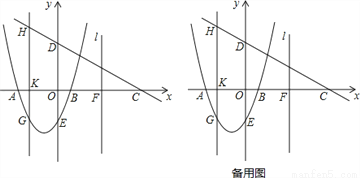
如图,抛物线y=ax2+bx-3交x轴于点A(﹣3,0),点B(1,0),交y轴于点E.点C是点A关于点B的对称点,点F是线段BC的中点,直线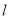 过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
过点F且与y轴平行.直线y=kx+3过点C,交y轴于D点.
(1)求抛物线的函数表达式;
(2)点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于点G,求线段HG长度的最大值;
(3)在直线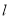 上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源:山东省济南市历城区2018届九年级上学期期末考试数学试卷 题型:单选题
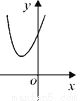
已知二次函数y = (x-m)2 +n的图象如图所示,则一次函数y = mx + n 与反比例函数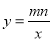 的图象可能是( )
的图象可能是( )
A. 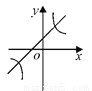 B.
B. 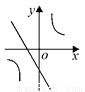 C.
C. 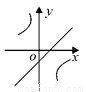 D.
D. 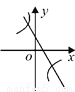
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县2017-2018学年七年级上期末统一质量检测数学试卷 题型:解答题
解方程: 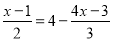
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com