
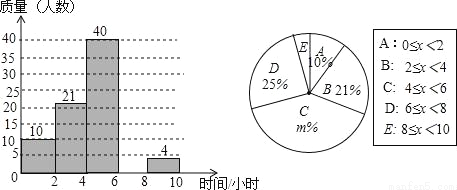
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
科目:初中数学 来源:福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型:解答题
分解因式: (1)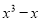 ; (2)
; (2)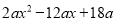 .
.
查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:解答题
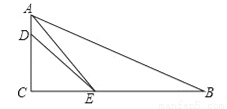
已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求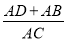 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:新疆阿克苏十二中2017-2018学年八年级(上)期中数学试卷 题型:单选题
等腰三角形两边长分别是3和8,则它的周长是( )
A. 14 B. 19 C. 11 D. 14或19
B 【解析】①若3是腰,则另一腰也是3,底是8,但是3+3<8,故不构成三角形,舍去. ②若3是底,则腰是8,8. 3+8>8,符合条件.成立. 故周长为:3+8+8=19. 故选:B.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
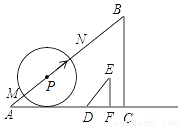
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60cm,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿
CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与直线AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中:
(1)连接ME,当ME∥AC时,t=________s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:填空题
已知抛物线y=x2-2mx-4 (m>0)的顶点 关于坐标原点
关于坐标原点 的对称点为
的对称点为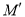 .若点
.若点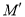 在这条抛物线上,则点M的坐标为_________.
在这条抛物线上,则点M的坐标为_________.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:单选题
如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x﹣m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标最大值为( )
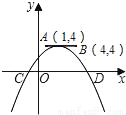
A. ﹣3 B. 1 C. 5 D. 8
D 【解析】当点C横坐标为-3时,抛物线顶点为A(1,4),对称轴为x=1,此时D点横坐标为5,则CD=8;当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);由于此时D点横坐标最大,故点D的横坐标最大值为8;故选D.查看答案和解析>>
科目:初中数学 来源:辽宁省鞍山市铁西区2017-2018学年七年级(上)期中数学试卷 题型:解答题
在数轴上表示下列各数,并用“>”连接起来.
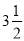 ,﹣|﹣4|,
,﹣|﹣4|, 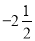 ,0,﹣1,﹣(﹣1)
,0,﹣1,﹣(﹣1)
查看答案和解析>>
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列计算正确的是( )
A. 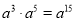 B.
B. 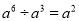 C.
C. 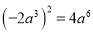 D.
D. 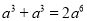
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com