
�����ǰϦ��С���ĸ�ĸ���������ɸ����Ӻ���Ѽ����ÿ�����ӵļ۸���ͬ��ÿ����Ѽ���ļ۸���ͬ������֪���ӵļ۸����Ѽ���ļ۸��1.8Ԫ����30Ԫ�������ӵĸ����뻨12Ԫ������Ѽ���ĸ�����ͬ������������Ѽ���ļ۸�����٣�
��Ѽ���ļ۸�Ϊ1.2Ԫ�����ӵļ۸�Ϊ3Ԫ�� ��������������������⿼���˷�ʽ���̵�Ӧ�ã��������⣬�ҵ���ȷ�ĵ�����ϵ�ǽ������Ĺؼ�������ĵ�����ϵΪ����30Ԫ�������ӵĸ����뻨12Ԫ������Ѽ���ĸ�����ͬ�� ��������Ѽ���ļ۸�ΪxԪ�������ӵļ۸�Ϊ��1��8+x��Ԫ�����ݻ�30Ԫ�������ӵĸ����뻨12Ԫ������Ѽ���ĸ�����ͬ���г���ʽ���̣�Ȼ��������̵Ľ⣬�õ�x��ֵ���ɣ� �������...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����������и�����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��������ż�����м�һ����n�������������ĺͣ��ú�n�Ĵ���ʽ��ʾ��
3n. ���������ɸ�����������ż�������ʽ��⣬�ֱ�ó�������ż����Ȼ��ӵ�һ����ͼ��ɣ� �������� ����������ż�����м�һ����n�� �����ż���Ķ����֪������������ż��Ϊn��2��n��n+2�� ��n��2+n+n+2=3n�� ���������ĺ�Ϊ3n���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ԭ��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
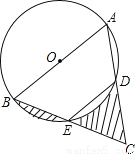
��ͼ��AB�ǡ�O��ֱ������EΪBC���е㣬AB=4����BED=120�㣬��ͼ����Ӱ���ֵ����֮��Ϊ�� ��
A��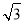 B��2
B��2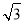 C��
C��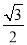 D��1
D��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����ػ�ͤ��2017~2018ѧ����꼶��ѧ���ϣ���ĩ���ģ���� ���ͣ������
��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�AB��AC�ϵĵ㣬��DE��BC������ADE���ABC���ܳ�֮��Ϊ2��3��AD��4����DB��_______��
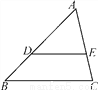
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����ػ�ͤ��2017~2018ѧ����꼶��ѧ���ϣ���ĩ���ģ���� ���ͣ���ѡ��
����˵������ȷ���� ( )
A. �� Rt��ABC����tanA��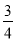 ����a��4��b��3
����a��4��b��3
B. �� Rt��ABC�У���C��90�㣬��tanA��tanB��1
C. �� Rt��ABC �У���C��90�㣬��a��3��b��4����tanA��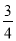
D. tan75�㣽tan(45�㣫30��)��tan45�㣫tan30�㣽1��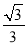
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ������
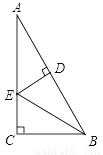
��ͼ����Rt��ACB�У���C=90�㣬BEƽ�֡�ABC��ED��ֱƽ��AB��D����AC=9����AE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ������
������y=��k+3��x|k|��2+4��һ�κ�������������ʽ��________��
y=6x+4�� ���������������� ��ԭ������һ�κ����ã� k+3��0 ��|k|��2=1����ã�k=3�����ԣ���������ʽ��y=6x+4�� �ʴ�Ϊ��y=6x+4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�������п���ѧģ���Ծ���4�·ݣ� ���ͣ������
��֪���κ���y=x2+bx+c��ͼ���㣨0��2���ͣ�1����1������ͼ��Ķ�������ͶԳ��ᣮ
���������ǣ�2����2�����Գ�����ֱ��x=2�� ����������������� Ҫ����κ����Ķ�������ͶԳ��ᣬ��Ҫ�õ����κ����Ľ���ʽ. ��Ϊ�����е�������ڸö��κ�����ͼ���ϣ�����������ĺ�������Ӧ������ö��κ����Ľ���ʽ. ����Ӧ����������ʽ�͵õ���һ�����ڴ���ϵ��b��c�Ķ�Ԫһ�η����飬����������øö��κ����Ľ���ʽ. ���ڸý���ʽ���϶��κ�����һ����ʽ������ͨ����ع�ʽ��ö�������ͶԳ�...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п���ѧģ���Ծ� ���ͣ������
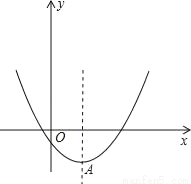
��֪���κ���y=x2��2mx+4m��8,
��1����x��2ʱ������ֵy��x���������С����m��ȡֵ��Χ��
��2����������y=x2��2mx+4m��8�Ķ���AΪһ���������������ߵ��ڽ���������AMN��M��N�����ڒ������ϣ������ʣ���AMN���������m�صĶ�ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɣ�
��3����������y=x2��2mx+4m��8��x�ύ��ĺ������Ϊ������������m����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com