
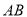 ,
, 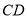 为⊙
为⊙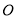 的两条弦,线段
的两条弦,线段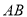 ,线段
,线段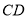 相交于点
相交于点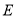 .
.
(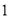 )若
)若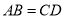 ,且
,且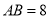 ,
, 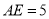 ,求
,求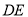 的长.
的长.
(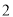 )若
)若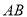 是⊙
是⊙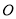 的直径,
的直径, 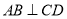 ,且
,且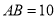 ,
, 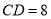 ,求
,求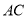 的长.
的长.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图,正方形网格中的每个小正方形边长都是 ,图中虚线叫做格线,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(只要求画出图形,不写作法和结
,图中虚线叫做格线,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(只要求画出图形,不写作法和结
论,作图需用黑笔描画):
( )使三角形为直角三角形,且不以格线为任意一边(在图
)使三角形为直角三角形,且不以格线为任意一边(在图 中画一个即可);
中画一个即可);
( )使三角形的三边长分别为
)使三角形的三边长分别为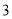 ,
, 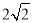 ,
, 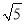 (在图
(在图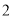 中画一个即可);
中画一个即可);
(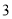 )使三角形为钝角三角形且面积为
)使三角形为钝角三角形且面积为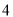 (在图
(在图 中画一个即可).
中画一个即可).


查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
下列关于x的方程有实数根的是( )
A. x2﹣x+1=0 B. x2+x+1=0 C. x2﹣x﹣1=0 D. (x﹣1)2+1=0
C 【解析】A、△=b2﹣4ac=1﹣4=﹣3<0,此方程没有实数根; B、△=b2﹣4ac=1﹣4=﹣3<0,此方程没有实数根; C、△=b2﹣4ac=1+4=5>0,此方程有两个不相等的实数根; D、△=b2﹣4ac=4﹣8=﹣4<0,此方程没有实数根. 故选:C.查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
(2013湖南娄底)使式子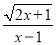 有意义的x的取值范围是( )
有意义的x的取值范围是( )
A. 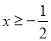 且x≠1
且x≠1
B. x≠1
C. 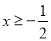
D. 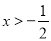 且x≠1
且x≠1
查看答案和解析>>
科目:初中数学 来源:湖北省宜昌市2018届九年级(上)期中数学试卷 题型:单选题
随着我国经济快速发展,轿车进入百姓家庭,小明同学在街头观察出下列四种汽车标志,其中既是中心对称图形,又是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:填空题
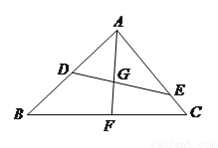
如图,在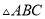 中,
中, 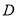 ,
, 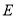 分别是
分别是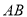 ,
, 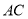 上的点,
上的点, 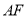 平分
平分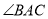 ,交
,交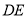 于点
于点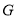 ,交
,交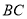 于点
于点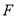 ,若
,若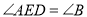 ,且
,且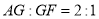 ,则
,则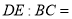 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:单选题
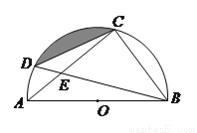
已知,如图,点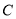 、
、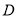 在⊙
在⊙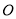 上,直径
上,直径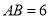 ,弦
,弦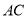 、
、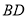 相交于点
相交于点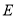 ,若
,若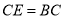 ,则阴影部分面积为( )
,则阴影部分面积为( )
A. 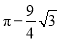 B.
B. 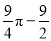 C.
C. 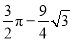 D.
D. 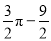
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:填空题
等腰三角形的一个内角是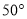 ,则它的底角是__________.
,则它的底角是__________.
查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图所示,一幅地图上有A,B,C三地,地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°方向,在B地的南偏东45°方向,你能确定C地位置吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com