
问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.
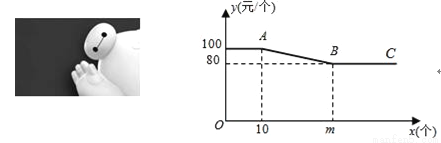
(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
(1)m=30,当一次销售数量超过30个以后,都是按单价80元/个销售; (2)当0<x≤10时,w=40x; 当10<x≤30时,w=﹣x2+50x; 当x>30时,w=20x; (3)店家应把最低价每个80元至少提高到每个85元. 【解析】 试题分析:(1)利用价格变化规律,进而求出m的值,然后根据解析式解释线段AB所表示的实际优惠销售政策即可; (2...科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,在四边形ABCD中,∠B=∠D=90°,AB=BC,AD=7,tan A=2.求CD的长.

查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
分式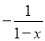 可变形为( )
可变形为( )
A. 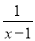 B.
B. 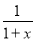 C.
C. 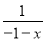 D.
D. 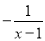
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )
A. B.
B.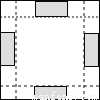 C.
C.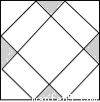 D.
D.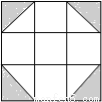
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
下列图形中,能通过折叠围成一个三棱柱的是 ( )
A. 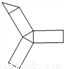 B.
B. 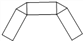
C. 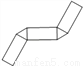 D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
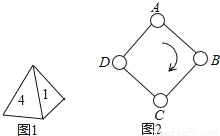
如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:填空题
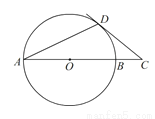
如图,AB是⊙O的直径,CD切⊙O于点D,若∠ =25°,则∠C=______°.
=25°,则∠C=______°.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
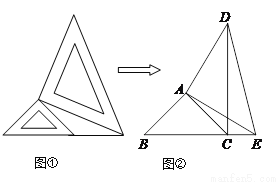
两个大小不同的等腰直角三角板如图①所示放置,图②是由它抽象出来的几何图形,点B、C、E在同一条直线上,连结DC.
(1)请找出图②中的全等三角形,并给予证明;
(2)求证:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城市八年级(上)期末数学试卷(五四学制) 题型:单选题
若关于x的方程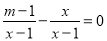 无解,则m的值是( )
无解,则m的值是( )
A. 3 B. 2 C. 1 D. ﹣1
B 【解析】解关于的方程得: , ∵原方程无解, ∴,即,解得: . 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com