
下列图案:

其中,中心对称图形是( )
A.①② B.②③ C. ②④ D.③④
D 【解析】 试题分析:根据中心对称图形的概念:绕某点旋转180°,能够与原图形完全重合的图形.可知①不是中心对称图形;②不是中心对称图形;③是中心对称图形;④是中心对称图形. 故选:D.科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
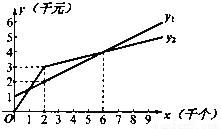
(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
(1)1;0.5;y=0.5x+1; (2)1.5; (3); (4)由图象可知,当x=8时,y1>y2,因此该单位选择乙厂更节省费用. 【解析】 试题分析:(1)由图得制版费是1千元,通过坐标(0,1)(2,2)求出函数解析式,印刷单价=(印刷费用-制版费)÷2000; (2)由图像可知,用3千元÷2千个,即可得到乙厂的平均印刷费; (3)设y2=kx+...查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:单选题
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=6cm,OD=4cm。则DC的长为
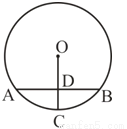
A、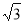 cm B、1cm C、2cm D、5cm
cm B、1cm C、2cm D、5cm
查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:填空题
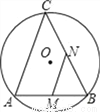
如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是____________.
查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
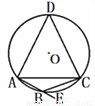
A. 130° B. 100° C. 65° D. 50°
C 【解析】∵∠CBE=50°,四边形ABCD是⊙O的内接四边形, ∴∠ADC=∠CBE=50°(圆内接四边形的一个外角等于内对角), ∵DA=DC, ∴∠DAC=∠DCA=. 故选C.查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
如图,A,B分别为CD,CE的中点,AE⊥CD于点A,BD⊥CE于点B.求∠AEC的度数.
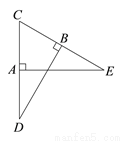
查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:填空题
如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程:____________.

查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
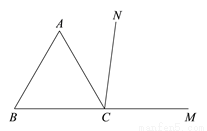
如图,CN是等边△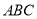 的外角
的外角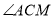 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若 ,求
,求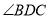 的大小(用含
的大小(用含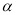 的式子表示);
的式子表示);
(3)用等式表示线段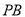 ,
, 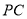 与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:填空题
若关于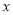 的方程
的方程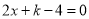 的解是
的解是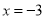 ,那么
,那么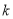 的值是________.
的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com