
��ͼ����ƽ��ֱ������ϵxOy�У���DEF���Կ����ǡ�ABC�������ɴε�ͼ�α仯����Գơ�ƽ�ƣ��õ��ģ�д��һ���ɡ�ABC�õ���DEF�Ĺ��̣�____________��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ��ʦ��棩����ĩ���1 ���ͣ���ѡ��
���һ������x1��x2������xn�ķ�����4������һ������x1+3��x2+3������xn+3�ķ����ǣ�������
A. 4 B. 7 C. 8 D. 19
A �������������������������ã�����x1��x2������xn��ƽ������Ϊa��������x1+3��x2+3������xn+3��ƽ����Ϊa+3�� ���ݷ��ʽ��S2= [(x1-a)2+(x2-a)2+��(xn-a)2]=4�� ������x1+3��x2+3������xn+3�ķ�� S2={[(x1+3)-(a+3)]2+[(x2+3)-(a+3)]2+��[(xn+3)-(a+3)] 2} ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡТ���а�У����2017-2018ѧ����꼶�ϲ���ѧ12�������Ծ� ���ͣ������
��ͼ����֪�ڡ�ABC�У���A=90��

��1������Բ���ֱ��������P��ʹԲ��P��AC���ϣ�����AB��BC���߶����У������� ͼ�ۼ�����д������֤������
��2������B=60�㣬AB=3�����P�������
��1����ͼ����������2��3�У� �������������������1����AB��BC���߶����У����ݽ�ƽ���ߵ����ʿ�֪Ҫ����ABC�Ľ�ƽ���ߣ���ƽ������AC�Ľ�����ǵ�P��λ�ã� ��2�����ݽ�ƽ���ߵ����ʺ�30��ǵ�ֱ�������ε����ʿ���뾶��Ȼ����Բ������� �����������1����ͼ��ʾ�����PΪ��������Բ�� ��2���ߡ�B=60�㣬BPƽ�֡�ABC�� ���ABP=30�㣬 ��AP=����S...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡТ���а�У����2017-2018ѧ����꼶�ϲ���ѧ12�������Ծ� ���ͣ���ѡ��
����ͼ����

���У����ĶԳ�ͼ���ǣ� ��
A���٢� B���ڢ� C. �ڢ� D���ۢ�
D �������� ����������������ĶԳ�ͼ�εĸ����ij����ת180�㣬�ܹ���ԭͼ����ȫ�غϵ�ͼ�Σ���֪�ٲ������ĶԳ�ͼ�Σ��ڲ������ĶԳ�ͼ�Σ��������ĶԳ�ͼ�Σ��������ĶԳ�ͼ�Σ� ��ѡ��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017-2018ѧ�������һѧ����ѧ��ĩ�Ծ� ���ͣ������
�ⷽ�̣� 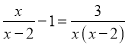 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017-2018ѧ�������һѧ����ѧ��ĩ�Ծ� ���ͣ������
��ͼ�����ı���ABCD�У���A=90�㣬��D=40�㣬���B+��CΪ__________��
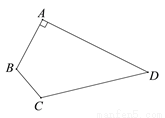
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������2017-2018ѧ�������һѧ����ѧ��ĩ�Ծ� ���ͣ���ѡ��
����ʽ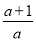 ��ֵ����0����
��ֵ����0����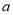 ��ֵΪ�� ��
��ֵΪ�� ��
A. 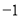 B. 1 C.
B. 1 C. 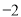 D. 2
D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������к�����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��֪��ABC�У�AB=2����C=40�㣬��������һ���ʵ���������ʹ��ABC����״�ʹ�С����ȷ���ģ������ӵ�������________________��
��A=60��(�𰸲�Ψһ) ����������֪һ�ߺ������ߵĶԽǣ�Ҫ��ȷ��Ψһ�������Σ�����������һ���ǣ�����AAS��ASA����Ψһȷ�������Σ������ӣ���A=60�㣬 �ʴ�Ϊ���𰸲�Ψһ���磺��A=60��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ��ѧ����ĩ����Ծ� ���ͣ������
��ͼ����֪������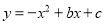 ��
��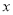 �ᡢ
�ᡢ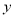 ��ֱ��ཻ�ڵ�A����1��0����B��0��3�����䶥��ΪD��
��ֱ��ཻ�ڵ�A����1��0����B��0��3�����䶥��ΪD��
(1)�����������ߵĽ���ʽ��
(2)����������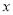 �����һ������ΪE�����ODE������������ߵĶԳ������Ƿ���ڵ�Pʹ�á�PAB���ܳ���̣��������������P�����꣬��������˵�����ɣ�
�����һ������ΪE�����ODE������������ߵĶԳ������Ƿ���ڵ�Pʹ�á�PAB���ܳ���̣��������������P�����꣬��������˵�����ɣ�
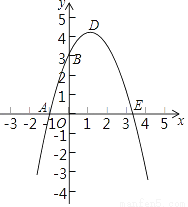
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com