
根据图中的程序计算y的值,若输入的x值为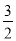 ,则输出的y值为( )
,则输出的y值为( )
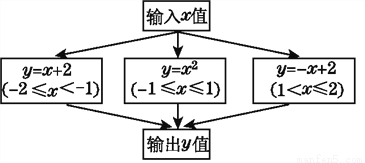
A. 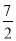 B.
B. 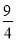 C.
C. 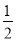 D.
D. 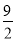
科目:初中数学 来源:2018人教版七年级数学下册练习:第五章达标检测卷 题型:单选题
直线l上有A、B、C三点,直线l外有一点P,若PA=5cm,PB=3cm,PC=2cm,那么点P到直线l的距离( )
A. 等于2cm B. 小于2cm
C. 小于或等于2cm D. 在于或等于2cm,而小于3cm
C 【解析】试题分析:直线外一点到直线上所有的点的连线当中,垂线段最短,故本题选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册同步要点3.2 用关系式表示的变量间关系 题型:单选题
如图,在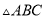 中,
中, 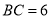 ,
, 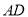 为
为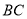 边上的高,
边上的高, 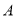 点沿
点沿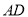 所在的直线运动时,三角形的面积发生变化,当
所在的直线运动时,三角形的面积发生变化,当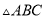 的面积为48时,
的面积为48时, 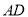 的长为( ).
的长为( ).

A. 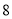 B.
B. 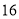 C.
C. 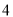 D.
D. 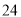
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:单选题
2x2y·(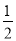 -3xy+y3)的计算结果是( )
-3xy+y3)的计算结果是( )
A. 2x2y4-x3y2+x2y B. -x2y+2x2y4
C. 2x2y4+x2y-6x3y2 D. -6x3y2+2x2y
C 【解析】2x2y·(-3xy+y3)= 2x2y·-2x2y·3xy+2x2y·y3= 2x2y4+x2y-6x3y2, 故选:C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型:解答题
如图,在三角形ABC中,底边BC=8 cm,高AD=6 cm,点E为AD上一动点,当点E从点D附近向点A运动时,三角形BEC的面积发生了变化.
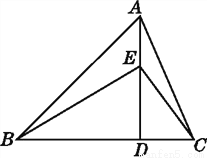
(1)在这个变化过程中,哪些量是变量?哪些量是常量?
(2)如果设DE的长为x cm,三角形BEC的面积为y cm2,那么怎样用含x的式子表示y?
(1)底边BC的长是常量,DE的长和三角形BEC的面积是变量(2)y=4x(0查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型:单选题
一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )
A. y=x(15-x) B. y=x(30-x) C. y=x(30-2x) D. y=x(15+x)
A 【解析】∵长方形的周长为30,其中一边长为, ∴该长方形的另一边长为: , ∴该长方形的面积: . 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:解答题
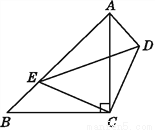
如图,△ABC,△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,试说明:△CDA≌△CEB.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
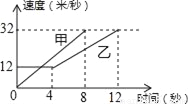
A. 乙前4秒行驶的路程为48米
B. 在0到8秒内甲的速度每秒增加4米/秒
C. 两车到第3秒时行驶的路程相等
D. 在4至8秒内甲的速度都大于乙的速度
C 【解析】试题分析:A.根据图象可得,乙前4秒行驶的路程为12×4=48米,正确; B.根据图象得:在0到8秒内甲的速度每秒增加4米秒/,正确; C.根据图象可得两车到第3秒时行驶的路程不相等,故本选项错误; D.在4至8秒内甲的速度都大于乙的速度,正确; 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型:单选题
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
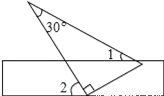
A. 60° B. 50° C. 40° D. 30°
D 【解析】先根据直角三角板的性质得出∠AFE的度数,再根据平行线的性质求出∠2的度数即可. 【解析】 如图所示, ∵△GEF是含45°角的直角三角板, ∴∠GFE=45°, ∵∠1=25°, ∴∠AFE=∠GEF﹣∠1=45°﹣25°=20°, ∵AB∥CD, ∴∠2=∠AFE=20°. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com