
直角三角形两直角边边长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )
A. 10cm B. 3cm C. 4cm D. 5cm
D 【解析】如图所示,在RT△ABC中,BC=6,AC=8,根据勾股定理得: AB==10, 又D、E是两直角边的中点,所以DE=AB=5.故选D. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:内蒙古2018届九年级(上)期中数学试卷 题型:解答题
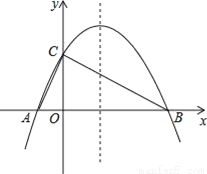
如图,已知抛物线y=﹣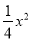 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为(﹣2,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为(﹣2,0).
(1)求抛物线的解析式;
(2)连接AC、BC,求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点P,使△ACP为等腰三角形?若存在,求出符合条件的P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型:填空题
已知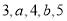 这五个数据,其中
这五个数据,其中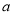 、
、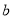 是方程
是方程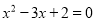 的两个根,则这五个数据的极差是____.
的两个根,则这五个数据的极差是____.
查看答案和解析>>
科目:初中数学 来源:四川省数学八年级下册期末复习测试卷 题型:解答题
如果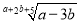 为a-3b的算术平方根,
为a-3b的算术平方根, 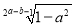 为1-a2的立方根,求2a-3b的平方根.
为1-a2的立方根,求2a-3b的平方根.
查看答案和解析>>
科目:初中数学 来源:四川省数学八年级下册期末复习测试卷 题型:单选题
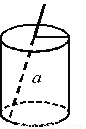
如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分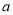 的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. 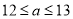 B.
B. 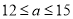
C. 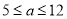 D.
D. 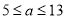
查看答案和解析>>
科目:初中数学 来源:四川省数学八年级下册期末复习测试卷 题型:单选题
下列命题是假命题的是( )
A. 平行四边形的对边相等 B. 四条边都相等的四边形是菱形
C. 矩形的两条对角线互相垂直 D. 等腰梯形的两条对角线相等
C 【解析】C项因为矩形的对角线相等但不一定垂直错误,是假命题;A、B、D选项正确,是真命题.查看答案和解析>>
科目:初中数学 来源:2017年广东省佛山市中考数学模拟试卷(3) 题型:解答题
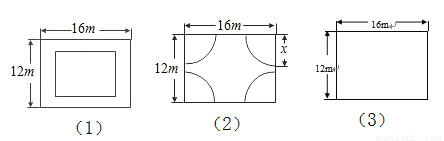
在一块长16m,宽12m的矩形荒地上建造一个花园,要求花轩占地面积为荒地面积的一半,下面分别是小强和小颖的设计方案.
(1)你认为小强的结果对吗?请说明理由.

(2)请你帮助小颖求出图中的x.
(3)你还有其他的设计方案吗?请在图(3)中画出一个与图(1)(2)有共同特点的设计草图,并加以说明.
查看答案和解析>>
科目:初中数学 来源:2017年广东省佛山市中考数学模拟试卷(3) 题型:单选题
下列图形中,只是中心对称图形的是( )
A. 圆 B. 角 C. 平行四边形 D. 等腰三角形
C 【解析】A选项中,因为圆既是中心对称图形也是轴对称图形,故本选项错误; B选项中,因为角不是中心对称图形,故本选项错误; C选项中,因为平行四边形只是中心对称图形,故本选项正确; D选项中,因为等腰三角形不是中心对称图形,故本选项错误; 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:解答题
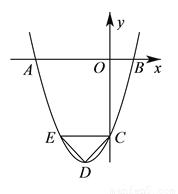
如图,抛物线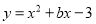 与
与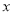 轴相交于
轴相交于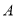 、
、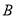 两点,与
两点,与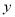 轴相交于点
轴相交于点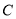 ,并且
,并且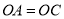 .
.
(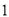 )求这条抛物线的关系式;
)求这条抛物线的关系式;
(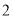 )过点
)过点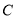 作
作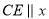 轴,交抛物线于点
轴,交抛物线于点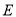 ,设抛物线的顶点为点
,设抛物线的顶点为点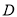 ,试判断
,试判断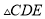 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com