
已知图中的两个三角形全等,则∠1等于( )
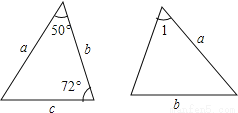
A.72° B.60° C.50° D.58°
D 【解析】 试题分析:根据三角形内角和定理求得∠2=58°;然后由全等三角形是性质得到∠1=∠2=58°. 【解析】 如图,由三角形内角和定理得到:∠2=180°﹣50°﹣72°=58°. ∵图中的两个三角形全等, ∴∠1=∠2=58°. 故选:D.科目:初中数学 来源:宁夏中卫市2018届九年级(上)期中数学试卷 题型:单选题
下列各组线段,能成比例的是( )
A. 3,6,9,18 B. 2,5,6,8 C. 1,2,3,4 D. 3,6,7,9
A 【解析】试题解析:A、3×18=6×9,故本选项正确; B、2×8≠5×6,故本选项错误; C、1×4≠2×3,故本选项错误; D、3×9≠6×7,故本选项错误. 故选A.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:单选题
已知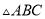 中,
中, 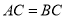 ,
, 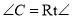 .如图,将
.如图,将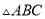 进行折叠,使点
进行折叠,使点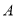 落在线段
落在线段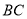 上(包括点
上(包括点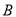 和点
和点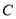 ),设点
),设点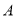 的落点为
的落点为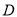 ,折痕为
,折痕为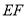 ,当
,当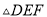 是等腰三角形时,点
是等腰三角形时,点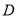 可能的位置共有( ).
可能的位置共有( ).

A. 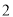 种 B.
种 B. 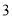 种 C.
种 C. 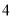 种 D.
种 D. 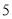 种
种
查看答案和解析>>
科目:初中数学 来源:广东省广州市番禺区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接AC并延长到点D,使CD =CA. 连接BC 并延长到点E,使CE =CB. 连接DE,那么量出DE的长就是A,B的距离.为什么?
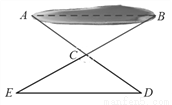
查看答案和解析>>
科目:初中数学 来源:广东省广州市番禺区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
2013年,我国上海和安徽首先发现“H7N9”新型禽流感病毒,此病毒颗粒呈多边形,其中球形病毒的最大直径为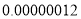 米,这一直径用科学计数法表示为____米.
米,这一直径用科学计数法表示为____米.
查看答案和解析>>
科目:初中数学 来源:广东省广州市番禺区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列交通标志是轴对称图形的是( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=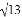 .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
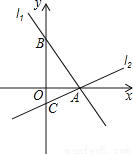
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系中,若点A(a,﹣b)在第一象限内,则点B(a,b)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D 【解析】∵点A(a,?b)在第一象限内, ∴a>0,?b>0, ∴b<0, ∴点B(a,b)所在的象限是第四象限。 故选D.查看答案和解析>>
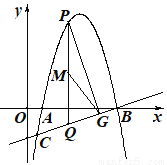
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在平面直角坐标系中,抛物线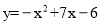 与直线
与直线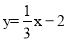 相交于点B、C,点P为直线BC上方的抛物线上的一动点, PQ⊥x轴交BC于点Q,PG⊥BC于点G,点M为线段PQ的中点,则线段GM的最大值为_________.
相交于点B、C,点P为直线BC上方的抛物线上的一动点, PQ⊥x轴交BC于点Q,PG⊥BC于点G,点M为线段PQ的中点,则线段GM的最大值为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com