
已知:平行四边形ABCD的两边AB、AD的长是关于x的方程x2﹣mx+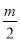 -
-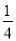 =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么平行四边形ABCD的周长是多少?
(1)m=1时,四边形ABCD是菱形,菱形ABCD的边长是;(2)平行四边形ABCD的周长是5. 【解析】试题分析: (1)∵四边形ABCD是菱形, ∴AB=AD, ∴△=0,即m2﹣4(﹣)=0, 整理得:(m﹣1)2=0, 解得m=1, 当m=1时,原方程为x2﹣x+=0, 解得:x1=x2=0.5, 故当m=1时,四边形ABCD是菱形,菱形的边...科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:解答题
(1)计算:1002-992+982-972+962-952+…+22-1;
(2)计算: 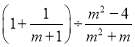 .
.
(3)因式分解:-4a2b+24ab-36b.
(1)5050;(2);(3). 【解析】试题分析: 首先数字分组,从第一个数起两两为一组,一正一负,进一步利用平方差公式分解,化为100+99+…+2+1,进一步计算求得结果即可. 根据分式混合运算步骤进行运算即可. 提公因式法和公式法相结合. 试题解析: (1)原式=(1002-992)+(982-972)+(962-952)+…+(22-1) =(100+...查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:单选题
在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A. 1枚 B. 2枚 C. 3枚 D. 任意枚
B 【解析】【解析】 ∵两点确定一条直线, ∴至少需要2枚钉子. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:单选题
如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
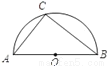
A. 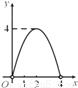 B.
B. 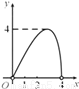 C.
C. 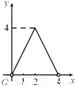 D.
D. 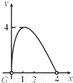
查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:单选题
若(2,5)、(4,5)是抛物线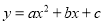 上的两个点则它的对称轴( )
上的两个点则它的对称轴( )
A. x=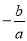 B.
B. 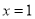 C.
C. 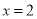 D.
D. 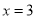
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:解答题
一只不透明的袋子中装有红球2个和白球2个,这些球除颜色外其余都相同,小明从袋子中任意摸出一球,记下颜色后不放回,若小明再从剩余的球中任取一球,请你用列表法或树状图的方法,求小明两次都摸出红球的概率.
【解析】试题分析:根据题意列出表格,然后根据表格求得全部情况的总数与符合条件的情况数目;二者的比值就是其发生的概率. 试题解析: 设红球分别为H1、H2,白球分别为B1、B2,列表得: 第二球 第一球 H1 H2 B1 B2 H1 (H1,H2) (H1,B1) (H1,B2) H2 (B1,H1) ...查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:填空题
如图是某地的灌溉系统,一个漂浮物A流到B处的概率为______.
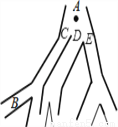
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古包头市七年级(下)期中数学试卷 题型:解答题
如图,在△ABC中,∠A=62°,∠B=74°,∠ACB的平分线交AB于D,DE∥BC交AC于E,求∠EDC的度数.
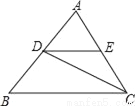
查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:单选题
下列性质中,矩形具有而菱形不一定具有的是( )
A. 对角线相等 B. 对角线互相平分
C. 对角线互相垂直 D. 邻边相等
A 【解析】菱形的性质有:四边形相等,两组对边分别平行,对角相等,邻角互补,对角线互相垂直且平分,且每一组对角线平分一组对角; 矩形的性质有:两组对边分别相等,两组对边分别平行,四个内角都是直角,对角线相等且平分; ∴矩形具有而菱形不一定具有的性质是对角线相等, 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com