练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，地面上两个村庄C、D处于同一水平线上，一飞行器在空中以6千米/小时的速度沿MN方向水平飞行，航线MN与C、D在同一铅直平面内．当该飞行器飞行至村庄C的正上方A处时，测得∠NAD=60°；该飞行器从A处飞行40分钟至B处时，测得∠ABD=75°．求村庄C、D间的距离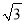（ 取1.73，结果精确到0.1千米）

    CD≈2.7千米． 【解析】试题分析：如图，过B作BE⊥AD于E，根据三角形的内角和定理可求得∠ADB=45°，根据直角三角形的性质得到AE=2．BE=2，求得AD=2+2，即可得到结论． 试题解析：过B作BE⊥AD于E， ∵∠NAD=60°，∠ABD=75°， ∴∠ADB=45°， ∵AB=6×=4， ∴AE=2．BE=2， ∴DE=BE=2， ∴...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年安徽省中考数学模拟试卷 题型：解答题

    已知在直角坐标平面内，抛物线y=x2+bx+c经过点A（2，0）、B（0，6）．

    （1）求抛物线的表达式；

    （2）抛物线向下平移几个单位后经过点（4，0）？请通过计算说明．

    （1）抛物线的表达式为y=x2﹣5x+6； （2）抛物线向下平移2个单位后经过点（4，0）． 【解析】试题分析：（1）代入A、B两点的坐标，根据待定系数法即可求得； （2）根据图象上下平移，只改变纵坐标，然后把经过的点的横坐标坐标代入函数解析式求得纵坐标，对比（4，0）即可求得． 【解析】 （1）把A（2，0），B（0，6）代入y=x2+bx+c 得 解得b=...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省鸡西市虎林市八五八农场学校2017-2018学年八年级（上）期中数学试卷 题型：解答题

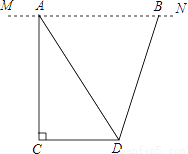
    在学习了全等三角形和等边三角形的知识后，张老师出了如下一道题：如图，点B是线段AC上任意一点，分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE，连接CD、AE分别与BE和DB交于点N、M，连接MN．求证：△ABE≌△DBC．

    接着张老师又让学生分小组进行探究：你还能得出什么结论？

    精英小组探究的结论是：AM=DN

    奋斗小组探究的结论是：△EMB≌△CNB．

    创新小组探究的结论是：MN∥AC．

    （1）你认为哪一小组探究的结论是正确的？

    （2）选择其中你认为正确的一种情形加以证明．

    （1）三个小组探究的结论都正确；（2）见解析 【解析】试题分析：由△ABD和△BCE是等边三角形，根据SAS易证得△ABE≌△DBC，由△ABE≌△DBC，可得∠EAC=∠NDB，又由∠ABD=∠MBN=60°，利用ASA，可证得△ABM≌△DBN，△EMB≌△CNB，又可证得△BMN是等边三角形，于是得到结论． 试题解析：（1）三个小组探究的结论都正确； （2）∵△ABD和△B...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省鸡西市虎林市八五八农场学校2017-2018学年八年级（上）期中数学试卷 题型：填空题

    计算：（﹣2a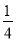）（a3）=_____．

    - 【解析】（﹣2a）（a3）=（﹣2×）a1+3=﹣a4， 故答案为：﹣a4.

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省鸡西市虎林市八五八农场学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

    根据下列条件，只能画出唯一的△ABC的是（　　）

    A. AB=3 BC=4 B. AB=4 BC=3 ∠A=30°

    C. ∠A=60°∠B=45° AB=4 D. ∠C=60°AB=5

    C 【解析】由所给边、角条件只能画出唯一的△ABC，说明当按所给条件画两次时，得到的两个三角形是全等的，即所给条件要符合三角形全等的判定方法；而在四个选项中，当两个三角形分别满足A、B、D三个选项中所列边、角对应相等时，两三角形不一定全等；当两个三角形满足C选项中所列边、角对应相等时，三角形是一定全等的. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级数学上期末复习检测数学试卷 题型：解答题

    某学校为美化校园，准备在长35米，宽20米的长方形场地上，修建若干条宽度相同的道路，余下部分作草坪，并请全校学生参与方案设计，现有3位同学各设计了一种方案，图纸分别如图l、图2和图3所示（阴影部分为草坪）．

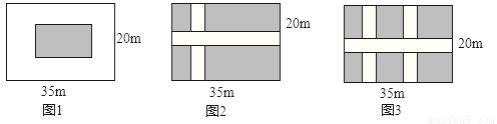
    请你根据这一问题，在每种方案中都只列出方程不解．

    ①甲方案设计图纸为图l，设计草坪的总面积为600平方米．

    ②乙方案设计图纸为图2，设计草坪的总面积为600平方米．

    ③丙方案设计图纸为图3，设计草坪的总面积为540平方米．

    见解析. 【解析】试题分析：①设道路的宽为x米．长应该为35﹣2x，宽应该为20﹣2x；那么根据草坪的面积为600m2 ，即可得出方程； ②如果设路宽为xm，草坪的长应该为35﹣x，宽应该为20﹣x；那么根据草坪的面积为600m2，即可得出方程； ③如果设路宽为xm，草坪的长应该为35﹣2x，宽应该为20﹣x；那么根据草坪的面积为540m2 ， 即可得出方程． 试题解析：①...

    查看答案和解析>>

    科目：初中数学 来源：湖南省2018届九年级数学上期末复习检测数学试卷 题型：填空题

    如图是两个形状相同的红绿灯图案，则根据图中给出的部分数值，得到x的值是________ 

    16 【解析】试题解析：∵两个红绿灯的形状相同， ∴， ∴x=16．

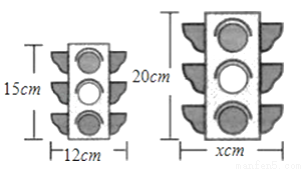
    查看答案和解析>>

    科目：初中数学 来源：湖北省十堰市2017-2018学年七年级（上）期中数学试卷 题型：解答题

    用简便方法计算：

    （1）﹣13×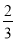﹣0.34×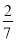+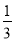×（﹣13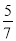）﹣×0.34，

    （2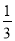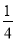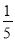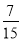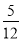）（﹣﹣+﹣+）×（﹣60）．

    （1）﹣13.34；（2）24． 【解析】试题分析: 先用交换律，然后应用乘法分配律，求出算式的值是多少即可． 应用乘法分配律，求出算式的值即可. 试题解析：（1）原式 （2）原式

    查看答案和解析>>

    科目：初中数学 来源：安徽省巢湖市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型：单选题

    如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上的点，将△ABC沿着DE折叠压平，A与A′重合，若∠A＝70°，则∠1＋∠2＝（　　）

    A. 110° B. 140° C. 220° D. 70°

    B 【解析】试题分析：∵四边形ADA′E的内角和为（4-2）•180°=360°， 而由折叠可知∠AED=∠A′ED，∠ADE=∠A′DE，∠A=∠A′， ∴∠AED+∠A′ED+∠ADE+∠A′DE=360°-∠A-∠A′=360°-2×70°=220°， ∴∠1+∠2=180°×2-（∠AED+∠A′ED+∠ADE+∠A′DE）=140°． 故选A．

    查看答案和解析>>

    同步练习册答案