
��ͼ��ֱ��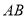 ��
��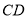 �ཻ�ڵ�
�ཻ�ڵ�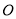 ��
�� 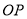 ��
��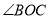 ��ƽ���ߣ�
��ƽ���ߣ� 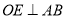 ��
�� 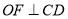 ��
��
��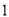 ��ͼ�г�ֱ���⣬������ȵĽ�����д�����ԣ�
��ͼ�г�ֱ���⣬������ȵĽ�����д�����ԣ�
��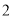 �����
�����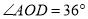 ����
����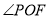 �Ķ�����
�Ķ�����
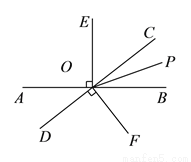
 ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017����꼶��ѧ���п���ģ��ѧ�Ծ� ���ͣ������
�Ƚ�����ʽ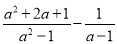 ���л���Ȼ������ѡ��һ������
���л���Ȼ������ѡ��һ������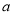 ��ֵ���������ʽ��ֵ.
��ֵ���������ʽ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ���ѡ��
��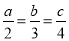 ����
����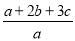 ���ڣ�������
���ڣ�������
A. 8 B. 9 C. 10 D. 11
C ������������������裬 ��a=2k��b=3k��c=4k�� ���� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ʡ��������������������꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ��������4�����ۣ���abc��0����b��a+c����4a+2b+c��0����b2��4ac��0��������ȷ�Ľ����У�������
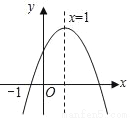
A. 1�� B. 2�� C. 3�� D. 4��
B ������������������������£���a��0���Գ�����y���ұߣ���b��0����y�ύ�������ᣬ��c��0����abc��0�������ȷ����x=��1ʱ��y��0����a��b+c��0����b��a+c�������ȷ����Ϊ�Գ���Ϊ1������=1���� 2a=��b����2a+b=0����۴���ͼ����x�����������㣬��4ac��0����ܴ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ʡ��������������������꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ����Rt��ABC�����С�B=35�㣬��C=90�㣩�Ƶ�A��˳ʱ�뷽����ת����AB1C1��λ�ã�ʹ�õ�C��A��B1��ͬһ��ֱ���ϣ���ô��ת�ǵ��ڣ�������
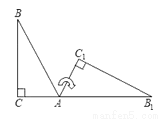
A. 55�� B. 70�� C. 125�� D. 145��
C ������������������ߡ�B=35�㣬��C=90�㣬���BAC=90�㩁��B=90�㩁35��=55�㣬�ߵ�C��A��B1��ͬһ��ֱ���ϣ� ���BAB��=180�㩁��BAC=180�㩁55��=125�㣬����ת�ǵ���125�㣮 ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݽ���2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��ͼ����֪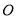 Ϊֱ��
Ϊֱ��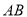 ��һ�㣬
��һ�㣬  ƽ��
ƽ��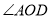 ��
�� 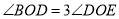 ��
�� 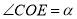 ����
����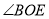 �Ķ���Ϊ_________�����ú�
�Ķ���Ϊ_________�����ú�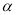 �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭���ݽ���2016-2017ѧ�����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ���ѡ��
��֪�߶�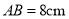 ����ֱ��
����ֱ��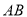 ����һ��
����һ��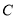 ����
����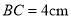 ����
����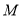 ���߶�
���߶�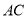 ���е㣬���߶�
���е㣬���߶�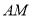 �ij�Ϊ�� ����
�ij��� ����
A. 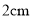 B.
B. 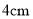 C.
C. 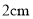 ��
��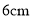 D.
D. 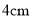 ��
��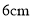
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²� ���в��Ծ� ���ͣ������
��������ֽƬ����ABC������ͼ��ʾ�ķ�ʽ�۵���ʹ��B���ڱ�AC�ϣ���Ϊ��B�䣬�ۺ�ΪEF����֪AB��AC��6��BC��8�����Ե�B�䣬F��CΪ��������������ABC���ƣ���BF�ij�����______
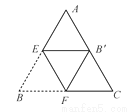
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰��ϲ��4�� ����ͼ�γ��� ��Ԫ���Ծ� ���ͣ������
��ͼ��������ֱ�����dzߵĶ��������һ��
(1)����DCE��35�㣬���ACB�Ķ�����
(2)����ACB��140�㣬���DCE�Ķ�����
(3)�����ACB���DCE�Ĺ�ϵ����˵�����ɣ�
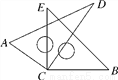
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com