
如果一条抛物线的形状与y=﹣2x2+2的形状相同,且顶点坐标是(4,﹣2),则它的解析式是________.
y=﹣2(x﹣4)2﹣2或y=2(x﹣4)2﹣2 【解析】试题解析:∵一条抛物线的形状与的形状相同, ∴a=±2, 设抛物线的顶点式为 ∵顶点坐标是(4,?2), ∴抛物线的顶点式为或 故答案为: 或科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:单选题
二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数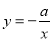 与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
与一次函数y=bx﹣c在同一坐标系内的图象大致是( )
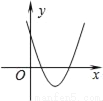
A. 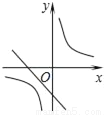 B.
B. 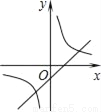 C.
C. 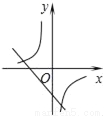 D.
D. 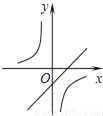
查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017年七年级上期期末数学试卷 题型:填空题
有理数2的相反数是________.
-2 【解析】由相反数的定义:“只有符号不同的两个数互为相反数”可知,2的相反数是-2.查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:解答题
现有形状、大小、颜色完全一样的三张卡片,上面分别标有数字“1”、“2”、“3”,第一次从这三张卡片中随机抽取一张,记下数字后放回;第二次在从这三张卡片中随机抽取一张并记下数字.请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽取的数字大于第一次抽取的数字的概率.
【解析】试题分析:首先根据题意画出树状图,由树状图即可求得所有等可能的结果与第二次抽取的数字大于第一次抽取的数字的情况,然后由概率公式即可求得答案. 试题解析:画树状图得: ∵共有9种等可能的结果,第二次抽取的数字大于第一次抽取的数字的有3种情况, ∴第二次抽取的数字大于第一次抽取的数字的概率为: =.查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
如图,△ABC与△DEF是位似图形,位似比为2:3,则△ABC与△DEF的面积比为 ________
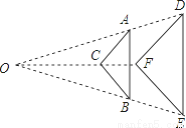
查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:单选题
如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则sin∠ACD=( )
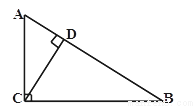
A. 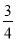 B.
B. 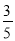 C.
C. 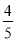 D.
D. 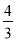
查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:解答题
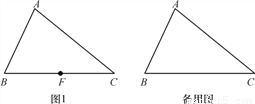
已知三角形ABC,EF∥AC交直线AB于点E,DF∥AB交直线AC于点D.
(1)如图1,若点F在边BC上,
①补全图形;
②判断∠BAC与∠EFD的数量关系,并给予证明;
(2)若点F在边BC的延长线上,(1)中的结论还成立吗?若成立,给予证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:单选题
若点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为( )
A. (0,5) B. (5,0)
C. (-5,0) D. (0,-5)
B 【解析】由题意得m-2=0,m=2,所以P(5,0),故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:填空题
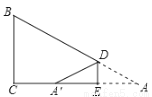
如图,在△ABC 中,∠C=90°,BC=6,D,E分别在AB、AC 上,将△ABC沿DE折叠,使点A落在点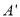 处,若
处,若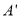 为CE的中点,则折痕DE的长为___________.
为CE的中点,则折痕DE的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com