
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:单选题
以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A. b≥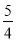 B. b≥1或b≤﹣1 C. b≥2 D. 1≤b≤2
B. b≥1或b≤﹣1 C. b≥2 D. 1≤b≤2
查看答案和解析>>
科目:初中数学 来源:2017年湖北省黄冈市中考数学二模试卷 题型:解答题
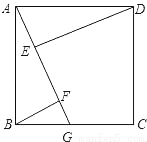
如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.
求证:AF=BF+EF.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省黄冈市中考数学二模试卷 题型:单选题
﹣9的相反数是( )
A. 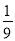 B. ﹣
B. ﹣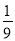 C. 9 D. ﹣9
C. 9 D. ﹣9
查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017年七年级上期期末数学试卷 题型:解答题
计算:
(1)( 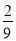 -
-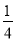 +
+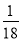 )÷(-
)÷(-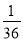 ); (2)-14-(-6)+2-3×(-
); (2)-14-(-6)+2-3×(-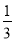 ).
).
查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017年七年级上期期末数学试卷 题型:单选题
如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A.5 cm B.1 cm C.5或1 cm D.无法确定
C 【解析】本题需要对以下两种情况分别进行讨论. (1) 点C不在线段AB上,则点C在线段AB的延长线上(如图①). 因为点M是AB的中点,AB=6cm,所以MB=3(cm). 因为点N是BC的中点,BC=4cm,所以BN=2(cm). 因此,MN=MB+BN=3+2=5(cm). (2) 点C在线段AB上(如图②). 因为点M是AB的中点,AB=6cm,...查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017年七年级上期期末数学试卷 题型:单选题
方程x+2=3的解是( )
A. 3 B. -3 C. 1 D. -1
C 【解析】试题分析:方程移项合并,即可求出解. 【解析】 方程x+2=3, 解得:x=1, 故选C查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
如果一条抛物线的形状与y=﹣2x2+2的形状相同,且顶点坐标是(4,﹣2),则它的解析式是________.
y=﹣2(x﹣4)2﹣2或y=2(x﹣4)2﹣2 【解析】试题解析:∵一条抛物线的形状与的形状相同, ∴a=±2, 设抛物线的顶点式为 ∵顶点坐标是(4,?2), ∴抛物线的顶点式为或 故答案为: 或查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2018届九年级(上)期中数学试卷(解析版) 题型:解答题
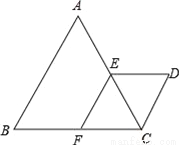
如图△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB.
(1)求证:四边形EFCD是菱形;
(2)设CD=4,求D、F两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com