
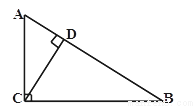
如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则sin∠ACD=( )
A. 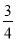 B.
B. 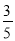 C.
C. 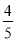 D.
D. 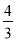
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:单选题
若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A. 矩形 B. 菱形
C. 对角线相等的四边形 D. 对角线互相垂直的四边形
D 【解析】由于E、F、G、H分别是AB、BC、CD、AD的中点, 根据三角形中位线定理得:EH ∥ FG ∥ BD,EF ∥ AC ∥ HG; ∵四边形EFGH是矩形,即EF⊥FG, ∴AC⊥BD,即对角线互相垂直, 故选D.查看答案和解析>>
科目:初中数学 来源:吉林省吉林市2016-2017年七年级上期期末数学试卷 题型:单选题
如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A.5 cm B.1 cm C.5或1 cm D.无法确定
C 【解析】本题需要对以下两种情况分别进行讨论. (1) 点C不在线段AB上,则点C在线段AB的延长线上(如图①). 因为点M是AB的中点,AB=6cm,所以MB=3(cm). 因为点N是BC的中点,BC=4cm,所以BN=2(cm). 因此,MN=MB+BN=3+2=5(cm). (2) 点C在线段AB上(如图②). 因为点M是AB的中点,AB=6cm,...查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
如图,∠BAD=∠C,DE⊥AB于E,AF⊥BC于F,若BD=6,AB=8,则DE:AF= .
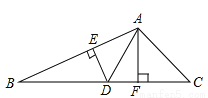
查看答案和解析>>
科目:初中数学 来源:吉林省长春市区2018届九年级上期末模拟数学试卷(解析版) 题型:填空题
如果一条抛物线的形状与y=﹣2x2+2的形状相同,且顶点坐标是(4,﹣2),则它的解析式是________.
y=﹣2(x﹣4)2﹣2或y=2(x﹣4)2﹣2 【解析】试题解析:∵一条抛物线的形状与的形状相同, ∴a=±2, 设抛物线的顶点式为 ∵顶点坐标是(4,?2), ∴抛物线的顶点式为或 故答案为: 或查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:解答题
如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
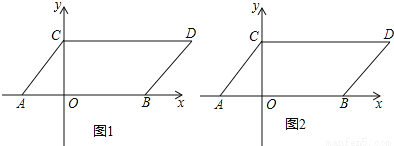
(1)写出点C,D的坐标并求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由;
(3)如图2,点P是直线BD上的一个动点,连接PC,PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD,∠POB的数量关系.
(1)C(0,2),D(4,2).8;(2)F(1,0)或(5,0);(3)当点P在线段BD上运动时:∠OPC=∠PCD+∠POB;当点P在BD延长线上运动时:∠OPC=∠POB-∠PCD;当点P在DB延长线上运动时:∠OPC=∠PCD-∠POB. 【解析】试题分析:(1)根据点平移的规律易得点C的坐标为(0,2),点D的坐标为(4,2);四边形ABDC的面积=2×(3+1)=8; (2)...查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:解答题
计算:
(1) 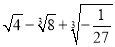 (2)
(2)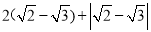
查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册(广西)期末测试 题型:单选题
已知实数a,b,若a>b,则下列结论错误的是( )
A. a-5>b-5 B. 3+a>b+3
C. 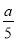 >
>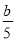 D. -3a>-3b
D. -3a>-3b
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(B卷) 题型:单选题
已知反比例函数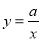 (
(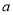 ≠0)的图象,在每一象限内,
≠0)的图象,在每一象限内, 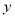 的值随
的值随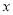 值的增大而减少,则一次函数
值的增大而减少,则一次函数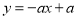 的图象不经过( )
的图象不经过( )
A. 第四象限 B. 第三象限
C. 第二象限 D. 第一象限
B 【解析】试题解析:∵反比例函数y=(a≠0)的图象在每个象限内y随x的增大而减小, ∴a>0, ∴-a<0, ∴一次函数y=-ax+a的图象经过第一、二、四象限,不经过第三象限. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com