
下面四个交通标志分别是步行标志、禁止行人通行标志、禁止驶入标志和直行标志,在这四个标志中,既是轴对称图形,又是中心对称图形的是( )

科目:初中数学 来源:初一数学第一学期6.1数据的收集 同步练习 题型:单选题
在设计调查问卷时,下面的提问比较恰当的是( )
A. 我认为猫是一种很可爱的动物
B. 难道你不认为科幻片比武打片更有意思
C. 你给我回答到底喜不喜欢猫呢
D. 请问你家有哪些使用电池的电器
D 【解析】A、我认为猫是一种很可爱的动物,这不是一个调查;B、难道你不认为科幻片比武打片更有意思?这也不是一个调查,这句话直接肯定了科幻片比武打片更有意思;C、你给我回答倒底喜不喜欢猫呢?这也不行;D、请问你家有哪些使用电池的电器?这是一个调查,可以设计调查问卷, 故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:单选题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线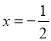 .下列结论中,正确的是( )
.下列结论中,正确的是( )
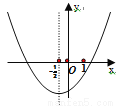
A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
D 【解析】由图象对称轴为直线x=-,则-=-,得a=b, A中,由图象开口向上,得a>0,则b=a>0,由抛物线与y轴交于负半轴,则c<0,则abc<0,故A错误; B中,由a=b,则a-b=0,故B错误; C中,由图可知当x=1时,y<0,即a+b+c<0,又a=b,则2b+c<0,故C错误; D中,由抛物线的对称性,可知当x=1和x=-2时,函数值相等,则当x=...查看答案和解析>>
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:填空题
如图,Rt△AOB绕点O逆时针转到△COD的位置,若旋转角是20°,则∠BOC的度数为____________.
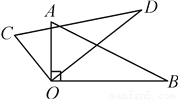
查看答案和解析>>
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:单选题
如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )
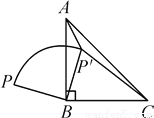
A. 1∶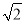 B. 1∶2 C.
B. 1∶2 C. 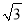 ∶2 D. 1∶
∶2 D. 1∶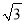
查看答案和解析>>
科目:初中数学 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知甲、乙二人解关于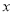 、
、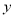 的方程组
的方程组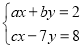 ,甲正确地解出
,甲正确地解出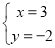 ,而乙把
,而乙把 抄错了,结果解得
抄错了,结果解得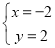 ,求
,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
关于x,y的方程组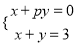 的解是
的解是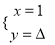 ,其中y的值被盖住了,不过仍能求出p,则p的值是( )
,其中y的值被盖住了,不过仍能求出p,则p的值是( )
A. ﹣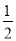 B.
B. 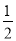 C. ﹣
C. ﹣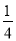 D.
D. 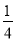
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:填空题
如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为 .
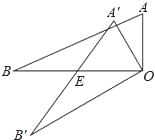
查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.

【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
-5 【解析】把代入方程得: ,解得: , ∴原方程为: ,解此方程得: , ∴此方程的另一根为: .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com