
已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
【答案】4π
【解析】试题解析:底面圆的半径为1cm,则底面周长=2πcm,底面积是πcm2 .
侧面面积=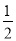 ×2π×3=3πcm2 .
×2π×3=3πcm2 .
则全面积=3π+π=4πcm2 .
点睛:圆锥的侧面积=底面周长×母线长÷2.
【题型】填空题
【结束】
12
已知扇形的圆心角为60°,半径为2,则扇形的弧长为________(结果保留π).
【解析】试题解析:依题意,n=60,r=2, ∴扇形的弧长= .科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:单选题
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
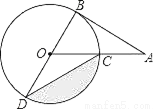
A. 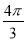 ﹣
﹣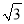 B.
B. 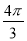 ﹣2
﹣2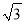 C. π﹣
C. π﹣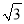 D.
D. 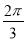 ﹣
﹣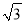
查看答案和解析>>
科目:初中数学 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
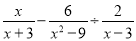
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, 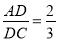 .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.
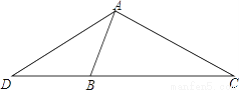
【答案】10
【解析】试题分析:根据相似三角形的判定定理得到△ADC∽△BAD,根据相似三角形的面积比等于相似比的平方即可得到结论.
试题解析:∵∠DAB=∠C,∠D=∠D, ∴△ADC∽△BAD,
∴ ,
,
∵△ADC的面积为18cm2 ,
∴△BDA的面积为8cm2 ,
∴△ABC的面积=△ADC的面积﹣△BDA的面积=10cm2
【题型】解答题
【结束】
24
如图,在网格图中的△ABC与△DEF是否成位似图形?说明理由.如果是,同时指出它们的位似中心.
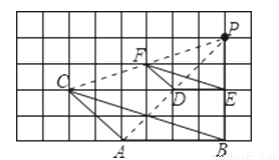
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
在等腰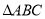 中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即
中,当顶角A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也确定了,我们把这个比值记作T(A),即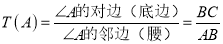 .例:T(60
.例:T(60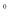 )=1,那么T(120
)=1,那么T(120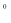 )=____________ ;
)=____________ ;
【答案】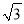
【解析】作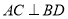 ,垂足为C.
,垂足为C.
设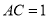
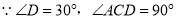
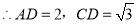
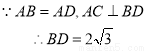
则T(120 )=
)=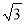
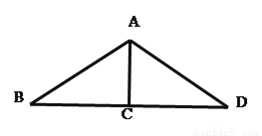
【题型】填空题
【结束】
17
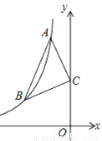
如图:已知点A、B是反比例函数y=﹣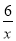 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:单选题
已知扇形的圆心角为45°,半径长为10,则该扇形的弧长为( )
A. 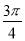 B.
B. 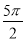 C. 3π D.
C. 3π D. 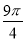
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.

(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
(1) (2)12 (3)相似三角形的基本知识推出该角度的相等,不能 【解析】 试题分析:(1)∵二次函数图象的顶点为P(4,-4),∴设二次函数的关系式为。 又∵二次函数图象经过原点(0,0),∴,解得。 ∴二次函数的关系式为,即。(2分) (2)设直线OA的解析式为,将A(6,-3)代入得,解得。 ∴直线OA的解析式为。 把x=4代入得y=...查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO 等于 ( )
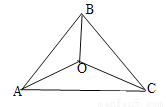
A. 1︰1︰1 B. 1︰2︰3 C. 2︰3︰4 D. 3︰4︰5
C 【解析】试题分析:首先过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F,由点O是△ABC内角平分线的交点,根据角平分线的性质,即可得OD=OE=OF,继而可得::=AB:BC:CA,则可求得答案. 过点O,作OD⊥AB于D,作OE⊥AC于E,作OF⊥BC于F, ∵点O是△ABC内角平分线的交点, ∴OD=OE=OF, ∴,,, ∵AB=20,BC...查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市汝城县濠头学校中考数学模拟试卷 题型:填空题
某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位.要求租用的车辆不留空座,也不能超载.有 种租车方案.
2 【解析】 试题分析:设租8座车x辆,4座车y辆,根据题意可得8x+4y=20,当x=1时,y=3;当x=2时,y=1,因此共有2种组车方案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com