
如果∠A是锐角,且sinA=cosA,那么∠A= ( )
A. 30° B. 45° C. 60° D. 90°
B 【解析】根据特殊角的三角函数值,可由∠A是锐角,且sinA=cosA,可知∠A=45°. 故选:B. 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
计算:(1) 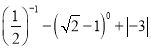
(2) 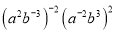
(3)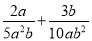
(4)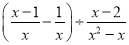
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
如图,在平面直角坐标系中,点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),按A→B→C→D→A…排列,则第2018个点所在的坐标是( )
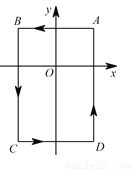
A. (1,1) B. (﹣1,1) C. (﹣1,﹣2) D. (1,﹣2)
B 【解析】∵2018÷4=504……2, ∴第2018个点所在的坐标是(﹣1,1). 故选B.查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在平面直角坐标系中,已知点A(2,0),B(2-a,0),C(2+a,0) (a>0),点P在以D(5,4)为圆心,半径为1的圆上运动,且始终满足∠BPC=90°,则a的最大值是________
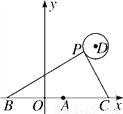
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=46°,则∠BCD等于( )

A. 34° B. 44° C. 46° D. 54°
B 【解析】根据直径所对的圆周角的性质,由AB是⊙O的直径,可得∠ADB=90°, 然后由∠ABD=46°,因此可知∠A=90°﹣∠ABD=44°;然后根据同弧所对的圆周角相等,可得∠BCD=∠A=38°. 故选:B.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
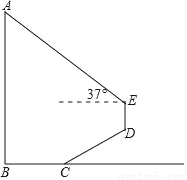
如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1: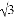 的斜坡CD前进2
的斜坡CD前进2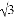 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,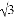 ≈1.73.)
≈1.73.)
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
如图,用长为10米的篱笆,一面靠墙(墙的长度超过10米),围成一个矩形花圃,设矩形垂直于墙的一边长为x米,花圃面积为S平方米,则S关于x的函数解析式是 (不写定义域).

查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10000元,第三天收到捐款12100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
(2)按照(1)中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
(1)10%;(2)33100. 【解析】试题分析:(1)解答此题利用的数量关系是:第一天收到捐款钱数×(1+每次增长的百分率)2=第三天收到捐款钱数,设出未知数,列方程解答即可; (2)第三天收到捐款钱数×(1+每次增长的百分率)=第四天收到捐款钱数,依此列式子解答即可. 试题解析:(1)设捐款增长率为x,根据题意列方程得, 10000×(1+x)2=12100, ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
下列二次根式中是最简二次根式的是( )
A. 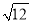 B.
B. 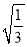 C.
C. 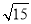 D.
D. 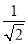
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com