练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

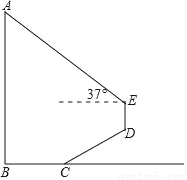
    如图，为测量学校旗杆AB的高度，小明从旗杆正前方3米处的点C出发，沿坡度为i=1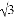：的斜坡CD前进2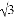米到达点D，在点D处放置测角仪，测得旗杆顶部A的仰角为37°，量得测角仪DE的高为1.5米．A、B、C、D、E在同一平面内，且旗杆和测角仪都与地面垂直．

    （1）求点D的铅垂高度（结果保留根号）；

    （2）求旗杆AB的高度（精确到0.1）．

    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75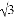，≈1.73．）

    （1）点D的铅垂高度是米（2）旗杆AB的高度约为7.7米 【解析】试题分析：（1）延长ED交射线BC于点H，根据坡度为1：，可得∠DCH =30°，由直角三角形中30°角所对的边等于斜边的一半，得DH=； （2）求出EF和FB的值，在Rt△AEF中，由正切求得AF的值，即可求得AB的值． 试题解析：（1）延长ED交射线BC于点H.由题意得DH⊥BC. 在Rt△CDH中，∠D...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市2017-2018学年第一学期初二数学期中试卷 题型：填空题

    若，则=______________

    11 【解析】∵ ∴ 故答案为：11

    查看答案和解析>>

    科目：初中数学 来源：北京市平谷区2018届初三第一学期期末数学试卷 题型：单选题

    下列各点在函数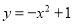图象上的是（　　）

    A. （0，0） B. （1，1） C. （0，﹣1） D. （1，0）

    D 【解析】A. 把（0，0）代入得，左=0，右=1 ，故不符合题意； B. 把（1，1）代入得，左=1，右=-1+1=0 ，故不符合题意； C. 把（0，﹣1）代入得，左=-1，右=1 ，故不符合题意； D. 把（1，0）代入得，左=0，右=-1+0=0 ，故不符合题意； 故选D.

    查看答案和解析>>

    科目：初中数学 来源：安徽省六安市2018届九年级上学期第二次月考数学试卷 题型：单选题

    如图，在△ABC，P为AB上一点，连结CP，下列条件中不能判定△ACP∽△ABC的是（ ）

    A. ∠ACP＝∠B B. ∠APC＝∠ACB C. D.

    D 【解析】由图可得∠A=∠A，又由有两角对应相等的三角形相似，即可得： 当∠ACP=∠B时，△ACP∽△ABC，故A不正确； 当∠APC=∠ACB时，△ACP∽△ABC，故B不正确； 当时，根据两边对应成比例，且夹角相等，可得△ACP∽△ABC，故C不正确；

    查看答案和解析>>

    科目：初中数学 来源：安徽省六安市2018届九年级上学期第二次月考数学试卷 题型：单选题

    如果∠A是锐角，且sinA=cosA，那么∠A＝　（ ）

    A. 30° B. 45° C. 60° D. 90°

    B 【解析】根据特殊角的三角函数值，可由∠A是锐角，且sinA=cosA，可知∠A=45°. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：上海浦东新区2017-2018学年九年级上学期期末数学试卷（初三一模） 题型：填空题

    已知点（-1，m）、（2，n）在二次函数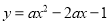的图像上，如果m>n，那么a 0（用“>”或“<”连接）．

    >； 【解析】∵=a(x-1)2-a-1， ∴抛物线对称轴为：x=1， 由抛物线的对称性，点（-1，m）、（0，n）在二次函数的图像上， ∵-1<0，m>n， ∴当x<-1时，y随x的增大而减小，所以a>0. 故答案为：>

    查看答案和解析>>

    科目：初中数学 来源：上海浦东新区2017-2018学年九年级上学期期末数学试卷（初三一模） 题型：填空题

    计算： = ．

    【解析】==. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：云南省2018届九年级上学期期中考试数学试卷 题型：解答题

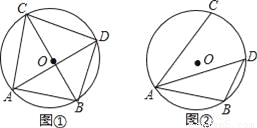
    已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D

    （1）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；

    （2）如图②，若∠CAB=60°，求BD的长．

    （1）AC=8，BD=CD=5；（2）5. 【解析】试题分析：(1)、根据直径得出∠CAB=∠BDC=90°，然后根据Rt△CAB的勾股定理得出AC的长度，然后根据等腰直角△BDC求出BD和CD的长度；(2)、连接OB，OD，根据AD平分∠CAB，且∠CAB=60°得出∠DOB=2∠DAB=60°，从而得出△OBD为等边三角形，从而得出BD的长度. 试题解析：(1)、如图①，∵BC是⊙...

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷（二） 题型：解答题

    如图所示，OE是∠AOD的平分线，OC是∠BOD的平分线．

    (1)若∠AOB＝130°，则∠COE是多少度？

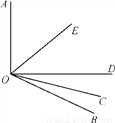
    (2)在(1)的条件下，若∠COD＝20°，则∠BOE是多少度？

    (1) 65°(2) 85° 【解析】试题分析：（1）直接根据角平分线的定义进行解答即可； （2）先根据∠COD=20°求出∠BOD的度数，再根据∠AOB=130°求出∠AOD的度数，根据角平分线的定义即可得出结论． 试题解析：（1）∵OC是∠AOD的平分线，OE是∠BOD的平分线，∠AOB=130° ∴∠COE=∠BOD+∠AOD=（∠BOD+∠AOD）=∠AOB=65°； ...

    查看答案和解析>>

    同步练习册答案