
方程(x-1)(x-2)=1的根是( )
A. x1=1,x2=2 B. x1=-1,x2=-2
C. x1=0,x2=3 D. 以上都不对
D 【解析】【解析】 方程整理得:x2﹣3x+1=0,这里a=1,b=﹣3,c=1,∵△=b2﹣4ac=9﹣4=5,∴x=.故选D.科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,数轴上的点A表示的数是-1,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
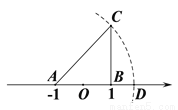
A. 2.8 B. 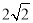 C.
C. 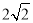 -
-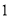 D.
D. 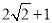
查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:填空题
对某校八年级(1)班50名同学的一次数学测验成绩进行统计,如果80.5—90.5分这一组的频数是18,那么这个班的学生这次数学测验成绩在80.5—90.5分之间的频率是____.
0.36 【解析】∵80.5—90.5分这一组的频数是18,该班总人数为50, ∴测验成绩在80.5—90.5分之间的频率为: . 故答案为: .查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:填空题
方程x2-3x+1=0的解是__________
【解析】观察原方程,可用公式法求解;首先确定a、b、c的值,在b2-4ac≥0的前提条件下,代入求根公式进行计算. 【解析】 a=1,b=-3,c=1, b2-4ac=9-4=5>0, x=; ∴x1=,x2=.查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:单选题
方程(x-4)(x+1)=1的根为( )
A. x=4 B. x=-1 C. x=4或x=-1 D. 以上都不对
D 【解析】【解析】 (x﹣4)(x+1)=1,整理得:x2﹣3x﹣5=0,b2﹣4ac=(﹣3)2﹣4×1×(﹣5)=9+20=29,x=,故选D.查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:单选题
一元二次方程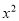 +2
+2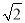 x-6=0的根是( )
x-6=0的根是( )
A. 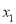 =
=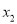 =
=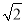 B.
B. 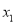 =0,
=0, 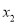 =-2
=-2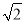
C. 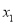 =
=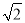 ,
, 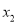 =-3
=-3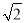 D.
D. 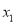 =-
=-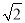 ,
, 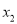 =3
=3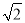
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:解答题
如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.
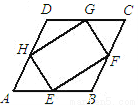
(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
(1)证明见解析.(2)证明见解析. 【解析】试题分析:(1)易证得△AEH≌△CGF,从而证得BE=DG,DH=BF.故有,△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证. (2)由题意知,平行四边形ABCD是菱形,连接AC,BD,则有AC⊥BD,由AB=AD,且AH=AE可证得HE∥BD,同理可得到HG∥AC,故HG⊥HE,又由(1)知四边形HGFE是平行四边形...查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:单选题
如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为( )
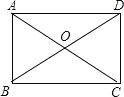
A. 10cm B. 8cm C. 6cm D. 5cm
D 【解析】试题解析:∵四边形ABCD是矩形, ∴OA=OC=AC,OD=OB=BD,AC=BD, ∴OA=OB, ∵AC+BD=20, ∴AC=BD=10cm, ∴OA=OB=5cm, ∵OA=OB,∠AOB=60°, ∴△OAB是等边三角形, ∴AB=OA=5cm, 故选D.查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
菱形的两条对角线长分别为9cm与4cm,则此菱形的面积为( )cm2.
A. 12 B. 18 C. 20 D. 36
B 【解析】试题分析:根据对角线的长可以求得菱形的面积, 根据S=ab=×4cm×9cm=18cm2, 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com