
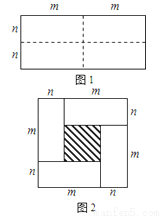
图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2, (m﹣n)2, mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:填空题
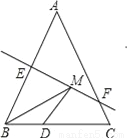
如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为_____cm.
查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:解答题
已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
(1)a=,方程的另一根为;(2)答案见解析. 【解析】试题分析:(1)把代入方程,求出的值,再把代入原方程,进一步解方程即可; (2)分两种情况探讨:①当时,为一元一次方程;②当时,利用 求出的值,再代入解方程即可. 试题解析:(1)将x=2代入方程(a-1)x2+2x+a-1=0,解得:a=. 将a=代入原方程得-x2+2x-=0,解得: ∴a=,方程的另一根为 ...查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:单选题
在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )
A. 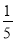 B.
B. 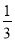 C.
C. 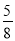 D.
D. 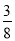
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
化简:|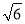 ﹣
﹣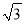 |﹣|3﹣
|﹣|3﹣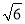 |.
|.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
已知长方体的体积为3a3b5cm3 , 它的长为abcm,宽为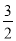 ab2cm,则这个长方体的高为________ cm.
ab2cm,则这个长方体的高为________ cm.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,已知AB∥CD,O是∠ACD和∠BAC的平分线的交点,若AC=6,S△AOC=6则AB与CD之间的距离是( ) 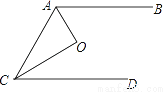
A. 1cm B. 2cm C. 3cm D. 4cm
C 【解析】过点0作AB的垂线,交AB于点D,交CD于点F,过O作OE垂直AC,交AC于点E,由题意得:OD=OE=OF, 6OE=12,解得OE=2,则DF=4.查看答案和解析>>
科目:初中数学 来源:山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
已知点(m,n)在抛物线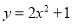 的图象上,则
的图象上,则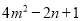 =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:解答题
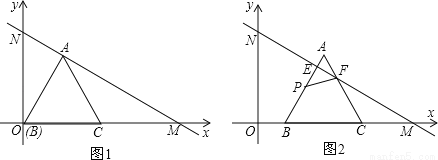
如图1,在平面直角坐标系xOy中,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6cm,∠OMN=30°,等边△ABC的顶点B与原点O重合,BC边落在x轴的正半轴上,点A恰好落在线段MN上,如图2,将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移,边AB、AC分别与线段MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s),△PEF的面积为S(cm2).
(1)求等边△ABC的边长;
(2)当点P在线段BA上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线B→A→C运动的过程中,是否在某一时刻,使△PEF为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com