练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知AB∥CD，O是∠ACD和∠BAC的平分线的交点，若AC=6，S△AOC=6则AB与CD之间的距离是（   ）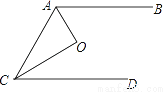

    A. 1cm B. 2cm C. 3cm D. 4cm

    C 【解析】过点0作AB的垂线，交AB于点D，交CD于点F,过O作OE垂直AC,交AC于点E，由题意得：OD=OE=OF， 6OE=12，解得OE=2，则DF=4.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：甘肃省武威市2017-2018学年八年级（上）期中数学试卷 题型：单选题

    已知直角三角形中30°角所对的直角边为2cm，则斜边的长为（　　）

    A. 2cm B. 4cm C. 6cm D. 8cm

    B 【解析】试题分析: 由题意可知，在直角三角形中，30°角所对的直角边等于斜边的一般，斜边=2×2=4cm.

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省韶关市南雄市中考数学模拟试卷 题型：填空题

    二次函数y=（x﹣1）2+2的最小值是_____．

    2 【解析】【解析】 ∵二次函数y=（x﹣1）2+2开口向上，其顶点坐标为（1，2）， ∴最小值是2．

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

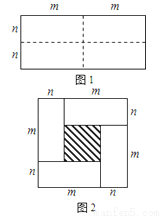
    图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

    （1）请写出图2中阴影部分的面积；

    （2）观察图2你能写出下列三个代数式之间的等量关系吗？

    代数式：（m+n）2， （m﹣n）2， mn；

    （3）根据（2）中的等量关系，解决如下问题：若a+b=7，ab=5，求（a﹣b）2的值．

    （1）（m﹣n）2或（m+n）2﹣4mn；（2）（m﹣n）2=（m+n）2﹣4mn；（3）29 【解析】试题分析：（1）方法一：求出正方形的边长，再根据正方形面积公式求出即可；方法二：根据大正方形面积减去4个矩形面积，即可得出答案；（2）根据两种表示阴影部分的面积的方法，即可得出等式；（3）根据等式（a-b）2=（a+b）2-4ab即可解决． 试题解析： （1）（m﹣n）2或（m...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

    命题“在角的内部，到角的两边距离相等的点在角的平分线上”的逆命题是：________

    角平分线上的点到角的两边距离相等 【解析】命题“在角的内部，到角的两边距离相等的点在角的平分线上”的逆命题是“角平分线上的点到这个角两边的距离相等”．

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级上期末模拟数学试卷 题型：单选题

    下列四边形中，对角线相等且互相垂直平分的是（   ）

    A. 平行四边形 B. 正方形 C. 等腰梯形 D. 矩形

    B 【解析】试题解析：对角线相等且互相垂直平分的四边形是正方形， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：解答题

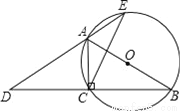
    如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

    （1）求证：∠B=∠D；

    （2）若AB=4，BC﹣AC=2，求CE的长．

    （1）证明见解析；（2）CE=1+. 【解析】试题分析：（1）由AB为⊙O的直径，易证得AC⊥BD，又由DC=CB，根据线段垂直平分线的性质，可证得AD=AB，即可得：∠B=∠D； （2）首先设BC=x，则AC=x-2，由在Rt△ABC中，AC2+BC2=AB2，可得方程：（x-2）2+x2=42，解此方程即可求得CB的长，继而求得CE的长． 试题解析：（1）证明：∵AB为⊙O的...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：单选题

    已知函数y＝kx＋b的图象如图，则一元二次方程x2＋x＋k－1＝0根的存在情况是(　　)

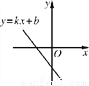
    A. 没有实数根; B. 有两个相等的实数根

    C. 有两个不相等的实数根; D. 无法确定

    C 【解析】试题分析：先根据函数y=kx+b的图象可得，k＜0，b＜0，再根据一元二次方程+x+k﹣1=0中，△=﹣4×1×（k﹣1）=5﹣4k＞0，则一元二次方程+x+k﹣1=0根的存在情况是有两个不相等的实数根. 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018学年度八年级第三次月考数学试卷 题型：填空题

    如图，在四边形ABCD中，AB∥DC，∠B=900，连接AC∠DAC=∠BAC.若BC=4cm，AD=5cm，则AB=_______cm.

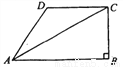
    8cm 【解析】过点D作DE⊥AB于点E， ∵在梯形ABCD中，AB∥CD， ∴四边形BCDE是矩形， ∴CD=BE，DE=BC=4cm，∠DEA=90°， ∴AE=cm， ∵AB∥CD， ∴∠DCA=∠BAC， ∵∠DAC=∠BAC， ∴∠DAC=∠DCA， ∴CD=AD=5cm， ∴BE=5cm， ∴AB=AE+BE=8c...

    查看答案和解析>>

    同步练习册答案