
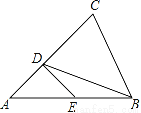
��ͼ��ʾ����D��AC�ϣ���E��AB�ϣ���AB=AC��BC=BD��AD=DE=EB�����A�Ķ�����
 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��26�� ���������� ��Ԫ���� ���ͣ������
������300ԪǮȫ��������Ӫ��Ʒ�������裬д�������ܹ���Ӫ��Ʒ������y��kg���뵥��x��Ԫ/kg��֮��Ĺ�ϵʽ����y��x�ĺ�����y��x�ķ�����������
y��x�ķ����������� �������������������������ֱ�ӵó�xy=300�������ó�y��x�ĺ�����ϵ�� ����������������� ������ɵã�xy=300���࣬y��x�ĺ�����y��x�ķ������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ�������ϱ�ʾ1��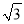 �Ķ�Ӧ��ֱ�Ϊ��A����B������A��BC���е㣬���C����ʾ����Ϊ �� ��
�Ķ�Ӧ��ֱ�Ϊ��A����B������A��BC���е㣬���C����ʾ����Ϊ �� ��
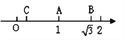
A. 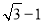 B.
B. 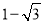 C.
C. 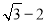 D.
D. 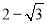
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��27�� ���� ��Ԫ���� ���ͣ���ѡ��
��������ͼ��һ�����Ƶ��ǣ�������
A. ���������ȱ������� B. ��������ֱ�������� C. ������������������ D. ������������
A �����������������A�����������ȱ�������һ�����ƣ��ʱ�ѡ����ȷ�� B����������ֱ�������β�һ�����ƣ��ʱ�ѡ����� C�������������������β�һ�����ƣ��ʱ�ѡ����� D�������������β�һ�����ƣ��ʱ�ѡ����� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�²���ѧ ��27�� ���� ��Ԫ���� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ�DE��BC����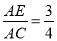 �� AD=9����AB���ڣ�������
�� AD=9����AB���ڣ�������
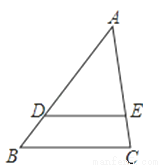
A. 10 B. 11 C. 12 D. 16
C ���������������������ƽ���߷��߶γɱ����������Եõ������AB�ij�. �����������DE��BC�� �࣬ ���� ��ã�AB=12. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ��һ�������ۺϲ��Ծ� ���ͣ������
��ͼ����֪��AOB=60�㣬��P��OA�ϣ�OP=8����M��N�ڱ�OB�ϣ�PM=PN����MN=2����OM= ��
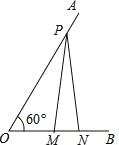
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ��һ�������ۺϲ��Ծ� ���ͣ���ѡ��
������x�IJ���ʽ��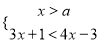 �Ľ⼯��x��4����a��ȡֵ��Χ�ǣ��� ����
�Ľ⼯��x��4����a��ȡֵ��Χ�ǣ��� ����
A. a��4 B. a��4 C. a��4 D. a��4
A ����������������� �� �ɢٵã�x��a�� �ɢڵã�x��4�� �߲���ʽ��Ľ⼯��x��4�� ��a��4�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����꼶�²���ѧ�����·�ʽ���ʽ���̵�Ԫ���� ���ͣ������
��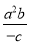 ��3•��
��3•��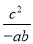 ��2�£�
��2�£�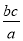 ��4=________��
��4=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����������ʮУ����2017-2018ѧ��Ȱ��꼶��һѧ����ĩ������ѧ�Ծ������ƣ� ���ͣ������
��һ��ֱ�����ǰ�DEF�����ڡ�ABC�ϣ����ǰ�DEF������ֱ�DZ�DE��DFǡ�÷ֱ���B��C����ABC�У���A=50�㣬���DBA+��DCA�Ķ�����
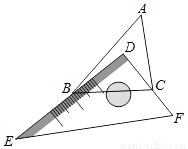
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com