
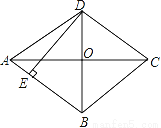
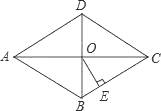
�ı���ABCD��ƽ���ı��Σ��Խ���ACƽ�֡�DAB��AC��BD�ཻ�ڵ�O��DE��AB��E�㣮��1����֤���ı���ABCD�����Σ�
��2����AC=8��BD=6����DE�ij��ȣ�
 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ɹ������첼�з�У���꼶���ϣ�������ѧ�Ծ� ���ͣ������
�����κ���y=x2��4x+5����y=��x��h��2+k����ʽ����y= ��
y=��x��2��2+1�� ��������y=x2-4x+5=x2-4x+4+1=(x-2)2+1.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���ξ��ж�ƽ���ı��β����е������ǣ�������
A. ����Ա߷ֱ�ƽ�� B. ����ԽǷֱ����
C. �Խ�����ƽ�� D. �Խ����ഹֱ
D �����������������A������ȷ������Ա߷ֱ�ƽ�У� B������ȷ������ԽǷֱ���ȣ����߾��д�������ȷ���� C������ȷ���Խ�����ƽ�֣����߾����д����ʣ� D�����εĶԽ����ഹֱ��ƽ���ı���ȴ�����ʣ� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�����꼶���£�������ѧ�Ծ� ���ͣ���ѡ��
һ���������ع�����ʻ�����ݣ�����ͼ���д����ܷ�ӳ����������ݵ�·��S��ǧ�ף�����ʻʱ��t��Сʱ���Ĺ�ϵ���ǣ�������
A. 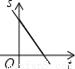 B.
B. 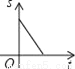 C.
C. 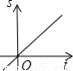 D.
D. 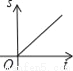
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�����꼶���£�������ѧ�Ծ� ���ͣ���ѡ��
���һ���ǵIJ�����150�㣬��ô����ǵ���ǵĶ����ǣ�������
A. 30�� B. 60�� C. 90�� D. 120��
B ��������180��-150��=30���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=8��BD=6��OE��BC������Ϊ��E����OE= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��֪���������ε����͵ij��ֱ���һԪ���η���x2��6x+8=0�ĸ�����������ε��ܳ�Ϊ��������
A. 8 B. 10 C. 8��10 D. 12
B ������������������ⷽ�̿ɵã�x=2��x=4���������ε����߳�Ϊ2��4��4�����ܳ�Ϊ��2+4+4=10.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŰ�ͷ�а��꼶���£�������ѧ�Ծ� ���ͣ������
������ʽx2+ax��2�ֽ���ʽ�Ľ��Ϊ��x+1����x��2������a��ֵΪ_____��
-1 ���������������� ��������ã�x2+ax��2=��x+1����x��2��=x2��x��2����a=��1���ʴ�Ϊ����1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��һ����ѧ��ȤС���У�С�����á�ͬ�����Ե�Բ�ܽǼ�Բ�Ľǵ����ʡ�̽����һЩ���⣬���������С��һ�����̽��֮�ã�
�����龳��
��1����ͼ1���ڡ�ABC�У���A=30�㣬BC=2�����ABC�����Բ�İ뾶Ϊ�� ����
����ʵ����
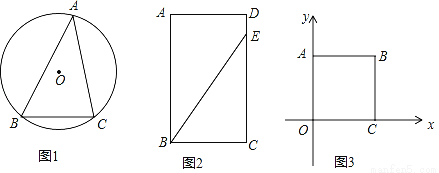
��2����ͼ2���ھ���ABCD�У����������ϲ�������õľ��飬�ھ���ABCD�ڲ���ֱ����Բ������һ��P����P���㣺��BPC=��BEC����PB=PC����Ҫ����ֱ����Բ��������P��������ͼ�ۼ�����
Ǩ��Ӧ�ã�
��3����ͼ3����ƽ��ֱ������ϵ�ĵ�һ��������һ��B������Ϊ��2��m��������B��AB��y�ᣬBC��x�ᣬ����ֱ�ΪA��C������P���߶�AB�ϻ�������P�������A��B�غϣ�������ʹ�á�OPC=45���λ������������m��ȡֵ��ΧΪ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com