练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

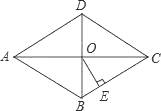
    如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE= ．

    . 【解析】试题解析：：∵四边形ABCD为菱形， ∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4， 在Rt△OBC中，∵OB=3，OC=4， ∴BC=， ∵OE⊥BC， ∴OE•BC=OB•OC， ∴OE=．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：单选题

    如图，△ABO中，AB⊥OB，OB=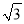，AB=1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1的坐标为

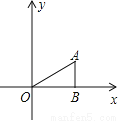
    A. （﹣1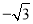， ） B. （﹣1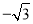， ）或（﹣2，0） C. 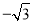（，﹣1）或（0，﹣2） D. 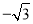（，﹣1）

    B 【解析】试题分析：需要分类讨论：在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标，即： ∵△ABO中，AB⊥OB，OB=，AB=1， ∴tan∠AOB=， ∴∠AOB=30°． 如图1，当△ABO绕点O顺时针旋转150°后得到△A1B1O， 则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°，...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古包头市七年级（下）期中数学试卷 题型：解答题

    补全下列推理过程：

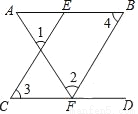
    如图，已知∠1=∠2，∠3=∠4，试说明AB∥CD．

    【解析】
    ∵∠1=∠2（已知）

    ∴CE∥FB （　 　）

    ∴∠4=∠AEC （　 　）

    ∵∠3=∠4 （ 已知）

    ∴∠3=∠AEC （　 　）

    ∴AB∥CD（　 　）

    同位角相等，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行 【解析】试题分析：先根据∠1=∠2，得出CE∥BF，进而得到∠4=∠AEC，再根据∠3=∠4，进而得到∠3=∠AEC，据此可得AB∥CD． 试题解析：【解析】 ∵∠1=∠2（已知） ∴CE∥FB（同位角相等，两直线平行 ） ∴∠4=∠AEC（两直线平行，同位角相等 ） ∵∠3=∠4 （...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古包头市七年级（下）期中数学试卷 题型：单选题

    如果每盒圆珠笔有12支，售价18元，用y（元）表示圆珠笔的售价，x表示圆珠笔的支数，那么y与x之间的关系应该是（ ）

    （A）y=12x （B）y=18x （C）y=x （D）y=x

    D 【解析】 试题分析：由题意知圆珠笔的单价是=（元/支），∴y=x； 故选D.

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型：解答题

    四边形ABCD是平行四边形，对角线AC平分∠DAB，AC与BD相交于点O，DE⊥AB于E点．（1）求证：四边形ABCD是菱形；

    （2）若AC=8，BD=6，求DE的长度．

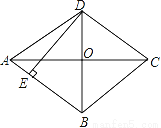
    (1)证明见解析；（2） 【解析】试题分析：（1）由对角线AC平分∠DAB证明平行四边形ABCD的邻边AB=BC即可证明四边形ABCD是菱形； （2）根据菱形的性质求得AB的长，再根据菱形面积的两种表示方式即可求解. 试题解析：（1）∵四边形ABCD是平行四边形，∴AD//BC，∴∠DAC=∠BCA， ∵AC平分∠DAB，∴∠DAC=∠BAC，∴∠BCA=∠BAC，∴AB=...

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型：单选题

    顺次连结对角线相等的四边形的四边中点所得图形是（　　）

    A. 正方形 B. 矩形 C. 菱形 D. 以上都不对

    C 【解析】试题解析：如图，E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点， 根据三角形的中位线定理，EF=AC，GH=AC，HE=BD，FG=BD， 连接AC、BD， ∵四边形ABCD的对角线相等， ∴AC=BD， 所以，EF=FG=GH=HE， 所以，四边形EFGH是菱形． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型：单选题

    一个盒子装有除颜色外其它均相同的2个红球和3个白球，现从中任取2个球，则取到的是一个红球、一个白球的概率为（　　）

    A. B. C. D.

    C 【解析】试题解析：画树状图得： ∵共有20种等可能的结果，取到的是一个红球、一个白球的有12种情况， ∴取到的是一个红球、一个白球的概率为：． 故选C．

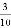
    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古包头市八年级（下）期中数学试卷 题型：单选题

    如果关于x的不等式（a+2014）x＞a+2014的解集为x＜l．那么a的取值范围是（　　）

    A. a＞﹣2014 B. a＜﹣2014 C. a＞2014 D. a＜2014

    B 【解析】【解析】 根据题意得：a+2014＜0，解得：a＜﹣2014．故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型：解答题

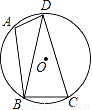
    如图，已知四边形ABCD内接于圆O，∠A=105°，BD=CD．

    （1）求∠DBC的度数；

    （2）若⊙O的半径为3，求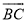的长．

    （1）75°；（2）π． 【解析】试题分析：（1）根据圆内接四边形的性质可得∠C的度数，然后根据等边对等角可得答案； （2）首先计算出∠BDC的度数，再根据圆周角定理可得∠BOC的度数，进而可得的长． 【解析】 （1）∵四边形ABCD内接于圆O， ∴∠DCB+∠BAD=180°， ∵∠A=105°， ∴∠C=180°﹣105°=75°， ∵BD=CD， ...

    查看答案和解析>>

    同步练习册答案