
��ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�2��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��25�ľ��루B��F��C��һ��ֱ���ϣ���
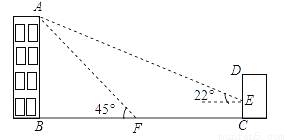
��1����칫¥AB�ĸ߶ȣ�
��2����Ҫ��A��E֮���һЩ���죬�������A��E֮��ľ��룮
���ο����ݣ�sin22���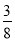 ��cos22���
��cos22���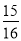 ��tan22���
��tan22���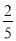 ��
��
 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017���������п���ѧ����Ծ� ���ͣ���ѡ��
����ͼ�Σ�����������Գ�ͼ�εĶԳ�������֮��Ϊ��������

A. 13 B. 11 C. 10 D. 8
B ����������һ��ͼ������Գ�ͼ�Σ���1���Գ�� �ڶ���ͼ������Գ�ͼ�Σ���2���Գ�� ������ͼ������Գ�ͼ�Σ���2���Գ�� ���ĸ�ͼ������Գ�ͼ�Σ���6���Գ�� ��������Գ�ͼ�εĶԳ�������֮��Ϊ11. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г����������Ծ���ѧ�Ծ� ���ͣ������
��ͼ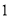 ���ڳ�����
���ڳ�����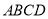 �У�
�� 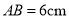 ��
�� 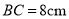 ����
����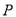 �ӵ�
�ӵ�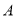 ��ʼ��
��ʼ��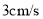 ���ٶ���
���ٶ���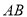 �����
�����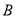 �˶�����
�˶�����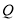 �ӵ�
�ӵ�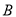 ��
��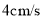 ���ٶ���
���ٶ���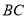 �����
�����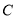 �˶������
�˶������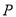 ��
��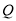 ͬʱ���������˶�ʱ��Ϊ
ͬʱ���������˶�ʱ��Ϊ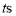 ��
��
��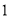 ����
����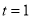 ʱ����
ʱ����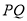 �ij���
�ij���
��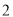 ������
������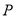 �˶�����
�˶�����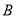 ʱ��
ʱ�� 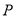 ��
��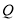 ͬʱֹͣ�˶������˶������У��Ƿ����
ͬʱֹͣ�˶������˶������У��Ƿ����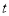 ��ֵ��ʹ��
��ֵ��ʹ��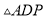 ��
��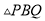 ��
��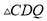 ���������ȣ������ڣ����
���������ȣ������ڣ����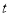 ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��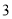 �����˶�
�����˶�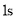 ʱ��
ʱ�� 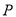 ��ֹͣ�˶���
��ֹͣ�˶��� 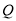 ����ԭ��������
����ԭ��������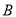 �㷵�أ��ڷ��صĹ����У�
�㷵�أ��ڷ��صĹ����У� 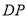 �Ƿ���ƽ��
�Ƿ���ƽ��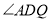 �����ܣ������
�����ܣ������ �˶���ʱ�䣻�����ܣ���˵�����ɣ�
�˶���ʱ�䣻�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г����������Ծ���ѧ�Ծ� ���ͣ���ѡ��
�Ѷ��θ�ʽ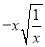 �и��������ʽ�Ƶ������ڣ�����ǣ� ����
�и��������ʽ�Ƶ������ڣ�����ǣ� ����
A. 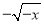 B.
B. 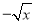 C.
C. 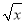 D.
D. 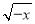
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г����������Ծ���ѧ�Ծ� ���ͣ���ѡ��
���и�ʽ�У���ȷ���ǣ� ����
A. 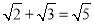 B.
B. 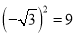 C.
C. 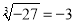 D.
D. 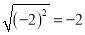
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ�2017���п���ѧ��ģ�Ծ� ���ͣ������
����ѧ���ϣ���ʦ����������⣺
��֪���߶�a��b��������������ABC��ʹAB=AC��BC=a��BC���ϵĸ�Ϊb����Ҫ�߹���ͼ��������ͼ�ۼ�����д������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ�2017���п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��2017�����ɹų������п���ѧ��ģ����֪��sin(��x)=��sinx�� cos(��x)=cosx��sin��x+y��=sinxcosy+cosxsiny�������и�ʽ���������ǣ� ��
A. cos����45�㣩= 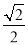 B. sin75��=
B. sin75��= 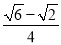
C. sin2x=2sinxcosx D. sin��x��y��=sinxcosy��cosxsiny
B ��������������Ŀ�����������㷽���ɵã�ѡ��A��cos����45�㣩=cos45��=��ѡ��B��sin75��=sin��30��+45�㣩=sin30��•cos45��+cos30��•sin45��=��+��=+��ѡ��C��sin2x=sinx•cosx+cosx•sinx=2sinx•cosx��ѡ��D��sin��x��y��=sinx•cos����y��+cosx•sin����y��=sinx•cosy��cosx•s...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ɹ��п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪����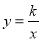 ��x��0����ͼ����A��B����B������Ϊ��2��2��������A��AC��x�ᣬ����ΪC������B��BD��y�ᣬ����ΪD��AC��BD���ڵ�F��һ�κ���y=ax+b��ͼ����A��D����x��ĸ����ύ�ڵ�E��
��x��0����ͼ����A��B����B������Ϊ��2��2��������A��AC��x�ᣬ����ΪC������B��BD��y�ᣬ����ΪD��AC��BD���ڵ�F��һ�κ���y=ax+b��ͼ����A��D����x��ĸ����ύ�ڵ�E��
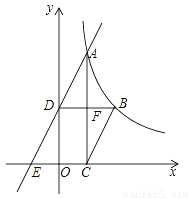
��1����AC=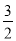 OD����a��b��ֵ��
OD����a��b��ֵ��
��2����BC��AE����BC�ij���
��1��a=��b=2����2��BC=�� �������������������1���������÷���������ͼ���ϵ���������ʵó�k��ֵ���ٵó�A��D�����꣬�������a��b��ֵ�� ��2����A�������Ϊ����m�� ������C�������Ϊ����m��0�����ó�tan��ADF=��tan��AEC=���������m��ֵ�����ɵó��𰸣� �����������1���ߵ�B��2��2���ں���y=��x��0����ͼ���ϣ� ��k=4����y=�� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ�2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���̣�m+2��x|m|+3mx+1=0�ǹ���x��һԪ���η��̣�������
A. m=��2 B. m=2 C. m=��2 D. m�١�2
B ������������һԪ���η��̵Ķ��壬��������������������1��δ֪������ߴ�����2����2��������ϵ����Ϊ0���ݴ˼�����⣮ �������� ��һԪ���η��̵Ķ���ɵ� �� ��ã�m=2�� ��ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com