
先化简,再求值: 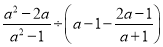 其中a是方程x2+2x=8的一个根.
其中a是方程x2+2x=8的一个根.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
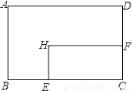
A. 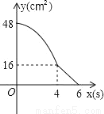 B.
B. 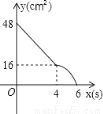 C.
C. 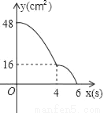 D.
D. 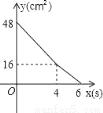
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
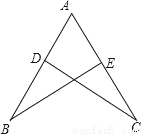
如图,点D,E分别在AB,AC上,且AD=AE,∠BDC=∠CEB.
求证:BD=CE.
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
若y=x+2﹣b是正比例函数,则b的值是( )
A. 0 B. ﹣2 C. 2 D. ﹣0.5
C 【解析】因为y=x+2﹣b是正比例函数,所以2-b=0,所以b=2,故选C.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型:解答题
某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价﹣成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值.
(1)y=2x+10;(2)p=﹣x2+2x+10;(3)当薄板的边长为25cm时,所获利润最大,最大值35元. 【解析】(1)利用待定系数法求一次函数解析式即可得出答案; (2)首先假设一张薄板的利润为p元,它的成本价为mx2元,由题意,得:p=y-mx2,进而得出m的值,求出函数解析式即可; (3)利用二次函数的最值公式求出二次函数的最值即可. 【解析】 (1)设一张薄板的边...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型:填空题
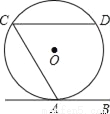
如图,直线AB与⊙O相切于点A,AC,CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为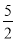 ,CD=4,则弦AC的长为_____.
,CD=4,则弦AC的长为_____.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型:单选题
将不等式组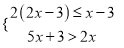 的解集在数轴上表示,下列表示中正确的是( )
的解集在数轴上表示,下列表示中正确的是( )
A. 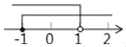 B.
B. 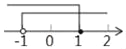 C.
C. 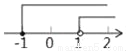 D.
D. 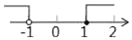
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上期末复习检测数学试卷 题型:填空题
如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1 ,A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是________.
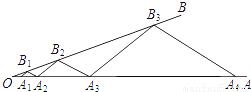
查看答案和解析>>
科目:初中数学 来源:青海省2018届九年级上学期12月月考数学试卷 题型:解答题
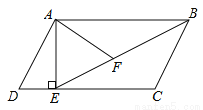
如图,在?ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=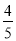 ,求AF的长.
,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com