
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:单选题
若我们把十位数字比个位和百位上的数字都大的三位数称为凸数,如:786,465,.则由1,2,3这三个数字构成的,数字不重复的三位数是“凸数”的概率是( )
A. 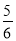 B.
B. 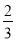 C.
C. 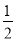 D.
D. 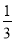
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第六章达标检测卷 题型:填空题
我们知道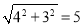 ,黄老师又用计算器求得:
,黄老师又用计算器求得: 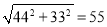 ,
, 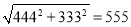 ,
, 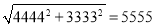 ,则计算:
,则计算: 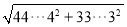 (2001个3,2001个4)=___________.
(2001个3,2001个4)=___________.
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:解答题
某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别 | 电视机 | 洗衣机 |
进价(元/台) | 1 800 | 1 500 |
售价(元/台) | 2 000 | 1 600 |
计划购进电视机和洗衣机共 100 台,商店最多可筹集资金161 800 元.
(1)请你帮助商店算一算有多少种进货方案(不考虑除进价之外的其他费用);
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最大的利润(利润=售价-进价).
(1)6(2) 购进电视机39台 【解析】(1)设购进电视x台,洗衣机就为(100-x)台,根据电视机的进价为1800元/台,洗衣机的进价为1500元/台,根据电视机进货量不少于洗衣机的进货量的一半,以及超市最多可筹集资金161800元可列不等式组求解. (2)设商店销售完毕后获利为 y 元,根据题意列出y与x的关系式,进行讨论 (1)设商店购进电视机 x 台,则购进洗衣机(10...查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:填空题
小明用100元钱去购买笔记本和钢笔共30分,已知每本笔记本2元,每枝钢笔5元,那么小明最多能买________枝钢笔.
13 【解析】分析:本题可设钢笔数为x,则笔记本有30-x件,根据小明用100元钱购得笔记本和钢笔共30件,就是已知不等关系:买笔记本用的钱数+买钢笔用的钱数≤100元.根据这个不等关系就可以得到一个不等式.求出钢笔数的范围. 解答:【解析】 设小明最多能买钢笔x支,依题意得 5x+2(30-x)≤100 解之得,x≤13 所以小明最多能买钢笔13支.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:单选题
若方程3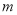 (
(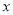 +1)+1=
+1)+1=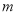 (3-
(3-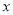 )-5
)-5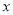 的解是负数,则
的解是负数,则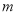 的取值范围是( )
的取值范围是( )
A.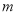 >-1.25 B.
>-1.25 B.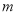 <-1.25 C.
<-1.25 C.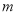 >1.25 D.
>1.25 D.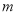 <1.25
<1.25
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:单选题
不等式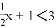 的正整数解有( ).
的正整数解有( ).
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】先求出不等式的解集,在取值范围内可以找到整数解. 【解析】 不等式的解集为x<4; 正整数解为1,2,3,共3个. 故选C. 解答此题要先求出不等式的解集,再确定正整数解.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.查看答案和解析>>
科目:初中数学 来源:湖北省鄂州市2017-2018学年七年级(上)期中数学试卷 题型:单选题
多项式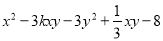 合并同类项后不含xy项,则k的值是( )
合并同类项后不含xy项,则k的值是( )
A. 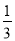 B.
B. 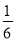 C.
C. 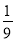 D. 0
D. 0
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷 题型:解答题
如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求直径AB的长.
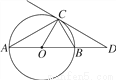
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com