
如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6 cm,BC=4 cm,试求线段DE的长;
(2)如果AB=a cm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC-BC=b cm,D,E分别为AC,BC的中点,你能猜想出线段DE的长度吗?写出你的结论,不用说明理由.
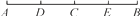
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:填空题
如果一个圆的面积是30 cm2,那么其中圆心角为60°的扇形面积是________cm2.
5 【解析】【解析】 圆心角为60°的扇形面积是: =5.故答案为:5.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
如图,射线OB,OC将∠AOD分成三部分,下列判断错误的是( ).

A.如果∠AOB=∠COD,那么∠AOC=∠BOD
B.如果∠AOB>∠COD,∠AOC>∠BOD
C.如果∠AOB<∠COD,∠AOC<∠BOD
D.如果∠AOB=∠BOC,∠AOC=∠BOD
D 【解析】 【解析】 由于∠AOB=∠BOC, 根据等式的性质,有∠AOB+∠BOC=∠BOC+∠BOC=2∠BOC, 即∠AOC=2∠BOC,而不是∠AOC=∠BOD.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
如图,军舰从港口沿OB方向航行,它的方向是( )
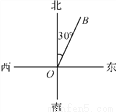
A. 东偏南30° B. 南偏东30° C. 南偏西30° D. 北偏东30°
D 【解析】【解析】 军舰从港口沿OB方向航行,它的方向是北偏东30°.故选D.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
如图中角的表示方法正确的个数有( )
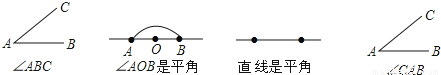
【选项】
A.1个
B.2个
C.3个
D.4个
B 【解析】 第一个图形应为∠CAB,表示错误;第二个图形∠AOB是平角正确;第三个图形,直线与平角是两个概念,平角有顶点,直线没有,表示错误;第四个图形,表示为∠CAB正确.综上所述,表示正确的有2个.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
已知线段a、b(a>b),用尺规作图法作一条线段,使其等于2a-b(不写作法,保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
(2012•葫芦岛)如图,C是线段AB上一点,M是线段AC的中点,若AB=8cm,BC=2cm,则MC的长是( )

A. 2 cm B. 3 cm C. 4 cm D. 6 cm
B 【解析】试题分析:由图形可知AC=AB﹣BC,依此求出AC的长,再根据中点的定义可得MC的长. 【解析】 由图形可知AC=AB﹣BC=8﹣2=6cm, ∵M是线段AC的中点, ∴MC=AC=3cm. 故MC的长为3cm. 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
小红家分了一套住房,她想在自己的房间的墙上钉一根细木条,挂上自己喜欢的装饰物,那么小红至少需要几根钉子使细木条固定( )
A. 1根 B. 2根 C. 3根 D. 4根
B 【解析】试题分析:根据两点确定一条直线这一基本事实即可解答. 【解析】 因为两点就可确定一条直线,所以需要两根钉子来固定. 故选B.查看答案和解析>>
科目:初中数学 来源:山东省诸城市2018届九年级上期末模拟数试卷 题型:解答题
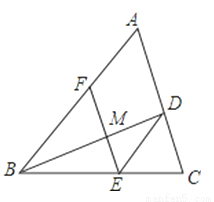
如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
(1)求证:BE=AF;
(2)设BD与EF交于点M,联结AE交BD于点N,求证:BN•MD=BD•ND.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com