
若方程组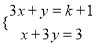 的解x,y满足0<x+y<1,则k的取值范围是( )
的解x,y满足0<x+y<1,则k的取值范围是( )
A. -4<k<0 B. -1<k<0 C. 0<k<8 D. k>-4
A 【解析】∵0科目:初中数学 来源:北师大版七年级数学下1.3同底数幂的除法 第2课时 零指数幂与负整数指数幂 同步练习 题型:单选题
下列计算正确的是( )
A.x2•x3=x5 B.x6+x6=x12 C.(x2)3=x5 D.x﹣1=x
A. 【解析】 试题分析:选项A,根据同底数幂的乘法可得原式=x5,正确;选项B,根据合并同类项法则可得原式=2x6,错误;选项C,根据幂的乘方可得原式=x6,错误;选项D,根据负整数指数幂法则原式=,错误,故答案选A.查看答案和解析>>
科目:初中数学 来源:2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型:解答题
当x取什么值时,代数式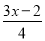 -2x+1的值为:(1)正数?(2)负数?(3)非负数?
-2x+1的值为:(1)正数?(2)负数?(3)非负数?
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:解答题
已知方程ax+12=0的解是x=3,求满足关于y的不等式(a+2)y<7的最小整数解.
关于y的不等式(a+2)y<7的最小整数解为﹣3. 【解析】试题分析:先将x=3代入ax+12=0,求出a的值,代入(a+2)y<7,再利用不等式的基本性质解不等式,然后从不等式的解集中找出适合条件的最小整数即可. 试题解析:将x=3代入ax+12=0, 得3a+12=0,解得a=﹣4. 把a=﹣4代入不等式,得﹣2y<7, 解得y>﹣3.5, 所以关于y的不等...查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:填空题
不等式组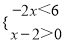 的解集是________.
的解集是________.
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:单选题
不等式2(x+1)<3x的解集在数轴上表示出来应为( ).
A. 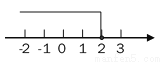 B.
B. 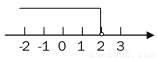
C. 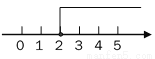 D.
D. 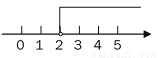
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《实际问题与二元一次方程组》同步练习 题型:解答题
某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
(1)甲种圆规每只的利润是4元,乙种圆规每只的利润是5元;(2)220. 【解析】试题分析:(1)设文具店销售甲、乙两种圆规,每只的利润分别是x元、y元,根据题意“销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元”,列出的方程组,解方程组即可;(2)根据题意可以列出文具店所获利p与a的函数关系式,然后根据当a≥30,可以求得p的最大值即可. 试题解...查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《消元解二元一次方程组》同步练习 题型:解答题
解方程(组):(1)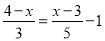 ; (2)
; (2)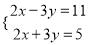
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:单选题
下列命题中,真命题是( )
A. 两条对角线相等的四边形是矩形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线互相平分的四边形是平行四边形
D 【解析】A.等腰梯形的对角线也相等,实际上可以任意旋转两条等长的相交线段,就能够得到无数对角线相等的四边形,但他们完全可以不是矩形,故A选项错误;B.如果一个四边形的对角线互相垂直,但是并没有互相平分的情形,只要让一条对角线平移,也可以得到无数不同的四边形,他们完全可以不是菱形,故B选项错误;C.只要适当选择角度,等腰梯形也可以满足题设条件,同样利用平移的技巧可以得到很多不同的四边形,故...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com