
方程3x2-2=1-4x的两个根的和为( )
A. 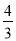 B.
B. 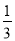 C. -
C. -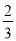 D. -
D. -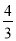
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版九年级下册数学 第二章 二次函数 单元检测卷 题型:解答题
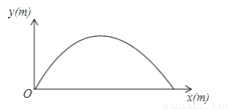
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=﹣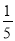 x2+
x2+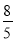 x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
(1)飞行的水平距离是多少时,球最高?
(2)球从飞出到落地的水平距离是多少?
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型:单选题
[(x2)3]7等于( )
A. -x7 B. x12 C. x9 D. x42
D 【解析】试题解析: 故D项正确. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:填空题
已知方程x2+mx+3=0的一个根是1,则它的另一个根是 ________,m的值是________ .
3 -4. 【解析】试题分析:根据韦达定理可得: ·==3,则方程的另一根为3;根据韦达定理可得: +=-=4=-m,则m=-4.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:单选题
一元二次方程x2﹣8x﹣1=0配方后可变形为( )
A. (x+4)2=17 B. (x﹣4)2=17 C. (x+4)2=15 D. (x﹣4)2=15
B 【解析】先移项可得x2﹣8x=1,再两边配上一次项系数一半的平方可得x2﹣8x+16=1+16,即(x﹣4)2=17. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:解答题
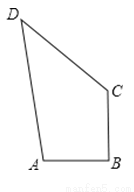
(6分)如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,DC=12,AD=13,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:填空题
如图,一扇卷闸门用一块宽18cm,长80cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起________cm.

查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:解答题
已知二次函数y=2x2﹣4mx+m2+2m(m是常数).
(1)求该函数图象的顶点C的坐标(用含m的代数式表示);
(2)当m为何值时,函数图象的顶点C在二、四象限的角平分线上?
(1)(m,﹣m2+2m);(2)m为0或3时 【解析】试题分析:(1)根据顶点坐标公式直接计算即可; (2)根据点C坐标,点C在直线y=-x上,即使横纵坐标互为相反数,计算即可得出答案. 试题解析:(1)由y=2x2-4mx+m2+2m =2(x2-2mx)+m2+2m =2(x-m)2-m2+2m, 得顶点C的坐标为(m,-m2+2m); (2)点C坐标(m,2m-...查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
如图,⊙O的直径AB垂直弦CD于点E,点F在AB的延长线上,且∠BCF=∠A.
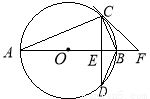
(1)求证:直线CF是⊙O的切线;
(2)若⊙O的半径为5,DB=4.求sin∠D的值.
(1)证明见解析;(2). 【解析】 试题分析:(1)连接OC,由OA=OA可知∠ACO=∠A,再根据∠FCB=∠A可知∠ACO=∠FCB,由于AB是⊙O的直径,所以∠ACO+∠OCB=90°故∠FCB+∠OCB=90°故可得出结论; (2)由AB是⊙O的直径,CD⊥AB可知 试题解析: (1)连接OC, ∵OA=OC, ∴∠ACO=∠A, 又∵∠FCB=...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com