
已知二次函数y=2x2﹣4mx+m2+2m(m是常数).
(1)求该函数图象的顶点C的坐标(用含m的代数式表示);
(2)当m为何值时,函数图象的顶点C在二、四象限的角平分线上?
(1)(m,﹣m2+2m);(2)m为0或3时 【解析】试题分析:(1)根据顶点坐标公式直接计算即可; (2)根据点C坐标,点C在直线y=-x上,即使横纵坐标互为相反数,计算即可得出答案. 试题解析:(1)由y=2x2-4mx+m2+2m =2(x2-2mx)+m2+2m =2(x-m)2-m2+2m, 得顶点C的坐标为(m,-m2+2m); (2)点C坐标(m,2m-...科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型:填空题
(-2a)2 -a2•a6 等于________ ;
4a2 -a8 【解析】试题解析: 故答案为:查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:单选题
方程3x2-2=1-4x的两个根的和为( )
A. 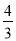 B.
B. 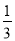 C. -
C. -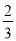 D. -
D. -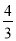
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:单选题
点P(m+3,m+2)在直角坐标系的y轴上,则点P的坐标为( )
A. (0,-1) B. (1,0) C. (3,0) D. (0,-5)
A 【解析】试题解析:∵点P(m+3,m+2)在直角坐标系的轴上, ∴m+3=0, 解得m=?3, ∴点P坐标为(0,-1), 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:单选题
一次函数y=k(x-1)的图象经过点M(-1,-2),则其图象与y轴的交点是( )
A. (0,-1) B. (1,0) C. (0,0) D. (0,1)
A 【解析】试题解析:把点M(-1,-2)代入一次函数y=k(x-1), 解得: 即 当时, 图象与y轴的交点是 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为_____.
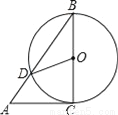
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:单选题
如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2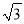 , OC=1,则圆O的半径为( )
, OC=1,则圆O的半径为( )
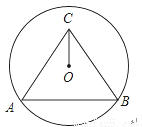
A. 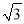 B. 2 C.
B. 2 C. 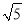 D.
D. 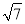
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.1 反比例函数 题型:填空题
双曲线y=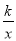 经过点(-2,3),则k=_______.
经过点(-2,3),则k=_______.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:填空题
如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是_______.
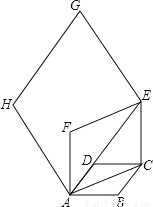
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com