
一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
(1);(2)P(两次摸到红球)=. 【解析】试题分析:(1)根据4个小球中红球的个数,即可确定出从中任意摸出1个球,恰好摸到红球的概率; (2)列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率. 试题解析:(1)4个小球中有2个红球, 则任意摸出1个球,恰好摸到红球的概率是; (2)列表如下: 红 红 ... 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:填空题
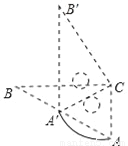
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为10cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长为______cm.
查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:单选题
点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A. 6 cm B. 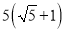 cm C.
cm C. 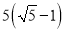 cm D.
cm D. 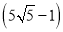 cm
cm
【答案】C
【解析】设AC= 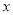 ,则BC=
,则BC= 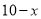 ,
,
∵点C是线段AB的黄金分割点(AC>BC),
∴AC2=BC AB,即
AB,即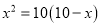 ,化简得:
,化简得: 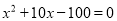 ,
,
解得: 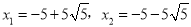 (不合题意,舍去).
(不合题意,舍去).
∴AC=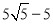 (cm).
(cm).
故选C.
点睛:本题解题的关键是要明白:“线段的黄金分割点把线段分成的两条线段中,较长的线段是较短线段和原线段的比例中项”.
【题型】单选题
【结束】
7
某养殖户的养殖成本逐年增长,第一年的养殖成本为12万元,第3年的养殖成本为16万元.设养殖成本平均每年增长的百分率为x,则下面所列方程中正确的是( )
A. 12(1﹣x)2=16 B. 16(1﹣x)2=12 C. 16(1+x)2=12 D. 12(1+x)2=16
D 【解析】由题意可得:第二年的养殖成本为, 第三年的养殖成本为: , ∴. 故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:填空题
周长为16cm的矩形的最大面积为______,此时矩形的边长为______,实际上此时矩形是________.
16cm2 4cm 正方形 【解析】设矩形一边长为xcm,另一边为(8-x)cm,则矩形面积,配方可得: ,当x=4时,矩形的面积最大,最大面积为:16,此时矩形是正方形,故答案为:16cm2,4cm,正方形.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第25章小结与复习 测试 题型:单选题
将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是( )
A. 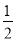 B.
B. 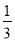 C.
C. 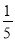 D.
D. 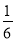
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:解答题
解方程:6﹣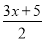 =
=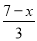 .
.
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:单选题
对于方程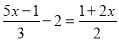 ,去分母后得到的方程是( )
,去分母后得到的方程是( )
A. 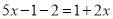 B.
B. 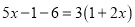
C. 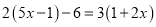 D.
D. 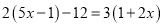
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:填空题
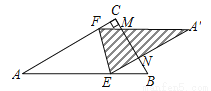
如图,已知△ABC中,∠C=90°,∠A=30°,AB=11,点E、F分别在AB、AC上,沿EF折叠△ABC,点A的对应点为点A′,A′E、A′F交BC于点M、N.若AE=8,当△A′MN与△ABC相似时,则AF =________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
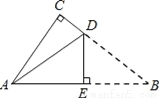
如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A. 4cm B. 5cm C. 6cm D. 10cm
B 【解析】试题分析:先根据勾股定理求出AB的长,再由图形折叠的性质可知,AE=BE,故可得出结论. ∵△ABC是直角三角形,两直角边AC=6cm、BC=8cm, ∴AB===10cm, ∵△ADE由△BDE折叠而成, ∴AE=BE=AB=×10=5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com