
点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A. 6 cm B. 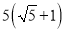 cm C.
cm C. 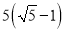 cm D.
cm D. 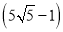 cm
cm
【答案】C
【解析】设AC= 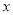 ,则BC=
,则BC= 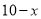 ,
,
∵点C是线段AB的黄金分割点(AC>BC),
∴AC2=BC AB,即
AB,即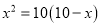 ,化简得:
,化简得: 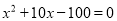 ,
,
解得: 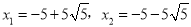 (不合题意,舍去).
(不合题意,舍去).
∴AC=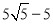 (cm).
(cm).
故选C.
点睛:本题解题的关键是要明白:“线段的黄金分割点把线段分成的两条线段中,较长的线段是较短线段和原线段的比例中项”.
【题型】单选题
【结束】
7
某养殖户的养殖成本逐年增长,第一年的养殖成本为12万元,第3年的养殖成本为16万元.设养殖成本平均每年增长的百分率为x,则下面所列方程中正确的是( )
A. 12(1﹣x)2=16 B. 16(1﹣x)2=12 C. 16(1+x)2=12 D. 12(1+x)2=16
D 【解析】由题意可得:第二年的养殖成本为, 第三年的养殖成本为: , ∴. 故选D.科目:初中数学 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
点P的横坐标是3,且到x轴的距离为5,则点P的坐标是______________;
(3,5)或(3,-5) 【解析】点P的纵坐标可能是5或-5,所以P的坐标是(3,5)或(3,-5). 故答案为(3,5)或(3,-5).查看答案和解析>>
科目:初中数学 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:填空题
在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A=________°。
36° 【解析】如图 设∠A=x. ∵AD=BD, ∴∠ABD=∠A=x; ∵BD=BC, ∴∠BCD=∠BDC=∠ABD+∠A=2x; ∵AB=AC, ∴∠ABC=∠BCD=2x, ∴∠DBC=x; ∵x+2x+2x=180°, ∴x=36°, ∴∠A=36° 故答案为:36°.查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,在 ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
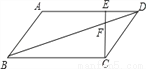
【答案】20
【解析】∵四边形ABCD是平行四边形,AE=4ED,
∴BC=AD=AE+ED=5ED,AD∥BC,
∴△DEF∽△BCF,
∴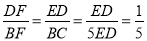 ,即
,即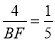 ,
,
∴BF=20.
【题型】填空题
【结束】
19
解方程:(1) 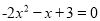 ; (2)
; (2)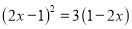 .
.
查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
若一元二次方程x2-x-1=0的两根分别为x1,x2,则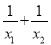 = .
= .
【答案】-1
【解析】∵一元二次方程: 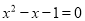 的两根是
的两根是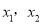 ,
,
∴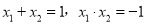 ,
,
∴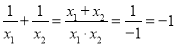 .
.
点睛:不解方程,求含有一元二次方程两根的代数式的值时,通常分两步完成:(1)由方程得到: 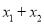 、
、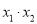 的值(前提是“根的判别式△
的值(前提是“根的判别式△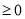 ”);(2)把要求值的代数式变形为用含“
”);(2)把要求值的代数式变形为用含“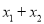 ”和“
”和“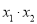 ”表达的形式,再代值计算即可.
”表达的形式,再代值计算即可.
【题型】填空题
【结束】
12
已知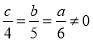 ,则
,则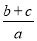 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:单选题
下列式子正确的是( )
A. 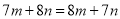 B.
B. 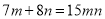
C. 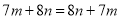 D.
D. 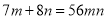
【答案】C
【解析】A选项中, 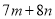 不一定等于
不一定等于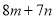 ,所以本选项错误;
,所以本选项错误;
B选项中, 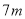 与
与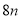 不是同类项,不能合并,所以本选项错误;
不是同类项,不能合并,所以本选项错误;
C选项中,根据加法的交换律, 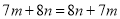 ,所以本选项正确;
,所以本选项正确;
D选项中, 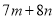 是求
是求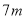 与
与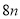 的和,不是求
的和,不是求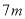 与
与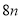 的积,所以本选项错误;
的积,所以本选项错误;
故选C.
【题型】单选题
【结束】
2
方程(x+1)(x﹣2)=0的解是( )
A. x=2 B. x=3 C. x1=﹣1,x2=3 D .x1=﹣1,x2=2
D 【解析】∵, ∴或, ∴解得: . 故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
已知△ABC中,BC=8,BC上高h=4,D为BC上一点,EF∥BC,交AB于点E,交AC于点F(E、F不过A、B),设E到BC的距离为x,则△DEF的面积y关于x的函数图象大致为(如图所示)()
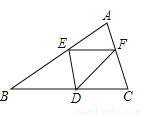
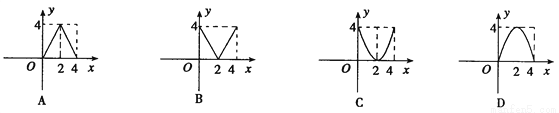
A. A B. B C. C D. D
D 【解析】过点A向BC作AH⊥BC于点H,所以根据相似比可知: , 即EF=,所以,故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第25章小结与复习 测试 题型:解答题
一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
(1);(2)P(两次摸到红球)=. 【解析】试题分析:(1)根据4个小球中红球的个数,即可确定出从中任意摸出1个球,恰好摸到红球的概率; (2)列表得出所有等可能的情况数,找出两次都摸到红球的情况数,即可求出所求的概率. 试题解析:(1)4个小球中有2个红球, 则任意摸出1个球,恰好摸到红球的概率是; (2)列表如下: 红 红 ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com