
下列运算正确的是( )
A. a2+a5=a7 B. (﹣a2)3=a6 C. a2﹣1=(a+1)(a﹣1) D. (a+b)2=a2+b2
C 【解析】A选项:a2+a5不能进行合并同类项,故A选项错误; B选项:(-a2)3=-a6,故B选项错误; C选项正确; D选项:(a+b))2=a2+2ab+b2,D选项错误. 故选C. 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
已知x2+3x﹣4=0,求代数式 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年七年级(上)期末复习数学试卷 题型:单选题
方程2x+1=3的解是( )
A. x=﹣1 B. x=1 C. x=2 D. x=﹣2
B 【解析】试题分析:移项,得2x=3﹣1,合并同类项,得2x=2,系数化为1,得x=1. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:填空题
某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是_____.
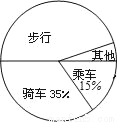
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:单选题
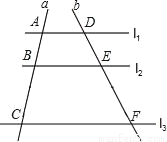
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若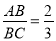 ,DE=4,则EF的长是( )
,DE=4,则EF的长是( )
A. 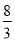 B.
B. 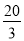 C. 6 D. 10
C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:解答题
如图1,两半径为r的等圆⊙O1和⊙O2相交于M,N两点,且⊙O2过点O1.过M点作直线AB垂直于MN,分别交⊙O1和⊙O2于A,B两点,连接NA,NB.
(1)猜想点O2与⊙O1有什么位置关系,并给出证明;
(2)猜想△NAB的形状,并给出证明;
(3)如图2,若过M的点所在的直线AB不垂直于MN,且点A,B在点M的两侧,那么(2)中的结论是否成立,若成立请给出证明.
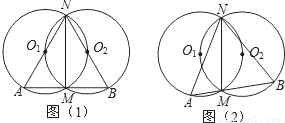
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学模拟试卷 题型:填空题
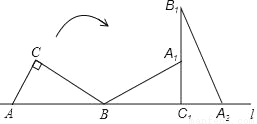
如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为_____.
查看答案和解析>>
科目:初中数学 来源:2017年天津109中中考数学模拟试卷 题型:解答题
(14分)如图,抛物线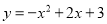 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
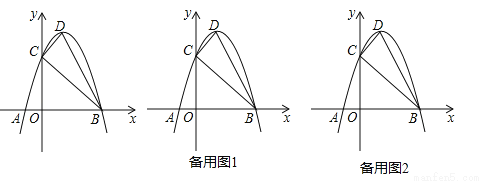
(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当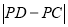 最大时,求a的值并在图中标出点P的位置;
最大时,求a的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
(1)C(0,3),D(1,4);(2)a=﹣3;(3)S=,当t=时,S有最大值. 【解析】试题分析:(1)令x=0,得到C的坐标,把抛物线配成顶点式,可得顶点D的坐标; (2)延长CD交x轴于点P.因为小于或等于第三边CD,所以当等于CD时, 的值最大.因此求出过CD两点的解析式,求它与x轴交点坐标即可; (3)过C点作CE∥x轴,交DB于点E,求出直线BD的解析式,得到点E...查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:单选题
若将点A(1,3)向左平移2个单位,再向下平移4个单位得到B,则点B的坐标为( )
A. (-2,-1) B. (-1,0) C. (-1,-1) D. (-2,0)
C 【解析】∵点A(1,3)向左平移2个单位,再向下平移4个单位得到点B, ∴点B的横坐标为1?2=?1,纵坐标为3?4=?1, ∴B的坐标为(?1,?1). 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com