在一个布口袋中装着只有颜色不同，其它都相同的白、红、黑三种颜色的小球各1只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球．

(1)试用树状图(或列表法)表示摸球游戏所有可能的结果；

(2)如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的概率．

如图，在直角坐标平面内，函数(x＞0，m是常数)的图象经过A(1，4)，B(a，b)，其中a＞1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连结AD，DC，CB．

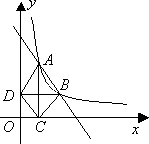
(1)若△ABD的面积为4，求点B的坐标；

(2)求证：DC∥AB；

(3)当AD＝BC时，求直线AB的函数解析式．

某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w(千克)随销售单价x(元/千克)的变化而变化，具体关系式为：w＝－2x＋240．设这种绿茶在这段时间内的销售利润为y(元)，解答下列问题：

(1)求y与x的关系式；

(2)当x取何值时，y的值最大？

(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克，公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？

如图①，已知抛物线的顶点为A(2，1)，且经过原点O，与x轴的另一交点为B．

(1)求抛物线的解析式；

(2)若点C在抛物线的对称轴上，点D在抛物线上，且以O、C、D、B四点为顶点的四边形为平行四边形，求D点的坐标；

(3)连接OA、AB，如图②，在x轴下方的抛物线上是否存在点P，使得△OBP与△OAB相似？若存在，求出P点的坐标；若不存在，说明理由．

某校为了了解全校2000名学生的课外阅读情况，在全校范围内随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，将结果绘制成频数分布直方图(如图所示)．

(1)这50名学生在这一天课外阅读所用时间的众数是多少？

(2)这50名学生在这一天平均每人的课外阅读所用时间是多少？

(3)请你根据以上调查，估计全校学生中在这一天课外阅读所用时间在1.0小时以上(含1.0小时)的有多少人？

如图，A、B分别为x轴和y轴正半轴上的点．OA、OB的长分别是方程x²－14x＋48＝0的两根(OA＞OB)，直线BC平分∠ABO交x轴于C点，P为BC上一动点，P点以每秒1个单位的速度从B点开始沿BC方向移动．

(1)设△APB和△OPB的面积分别为S₁、S₂，求S₁∶S₂的值；

(2)求直线BC的解析式；

(3)设PA－PO＝m，P点的移动时间为t．

①当0＜t≤时，试求出m的取值范围；

②当t＞时，你认为m的取值范围如何(只要求写出结论)？

如图1，在平面直角坐标系中，已知点A(0，4)，点B在x正半轴上，且∠ABO＝30°．动点P在线段AB上从点A向点B以每秒个单位的速度运动，设运时间t秒．在x轴上取两点M、N作等边三角形△PMN．

(1)求直线AB的解析式；

(2)求等边三角形△PMN的边长(用t的代数式表示)，并求出当等边三角形△PMN的顶点M运动到与原点O重合时t的值；

(3)如果取OB的中点D，艰OD为边在RtAOB内部作如图2所示的矩形ODCE，点C在线段AB上．设等边三角形△PMN和矩形ODCE重叠部分的面积为S，请你求出当0≤t≤2时S与t的函数关系式，并求出S的最大值．

如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过O作OH⊥AC于点H．若OH＝2，AB＝12，BO＝13．求：(1)⊙O的半径；(2)sin∠OAC的值；(3)弦AC的长(结果保留两个有效数字)．

两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED按图1所示的位置放置A与C重合，O与E重合．

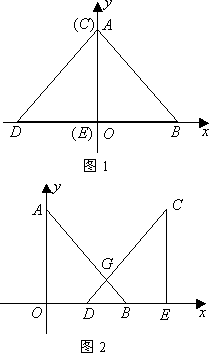
(1)求图1中，A，B，D三点的坐标．

(2)Rt△AOB固定不动，Rt△CED沿x轴以每秒2个单位长的速度向右运动，当D点运动到与B点重合时停止，设运动x秒后Rt△CED和Rt△AOB重叠部分面积为y，求y与x之间的函数关系式．

(3)当Rt△CED以(2)中的速度和方向运动，运动时间x＝4秒时RT△CED运动到如图2所示的位置，求经过A，G，C三点的抛物线的解析式．

(4)现有一半径为2，圆心P在(3)中的抛物线上运动的动圆，试问⊙P在运动过程中是否存在⊙P与x轴或y轴相切的情况，若存在请求出P的坐标，若不存在请说明理由．

如图，在平面直角坐标系xOy中，M是x轴正半轴上一点，⊙M与x轴的正半轴交于A，B两点，A在B的左侧，且OA，OB的长是方程x²－12x＋27＝0的两根，ON是⊙M的切线，N为切点，N在第四象限．

(1)求⊙M的直径．

(2)求直线ON的解析式．

(3)在x轴上是否存在一点T，使△OTN是等腰三角形，若存在请在图2中标出T点所在位置，并画出△OTN(要求尺规作图，保留作图痕迹，不写作法，不证明，不求T的坐标)若不存在，请说明理由．