如图，将·A＝6，AB＝4的矩形·ABC放置在平面直角坐标系中，动点M、N以每秒1个单位的速度分别从点A、C同时出发，其中点M沿A·向终点·运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交·B于点P，连接MP．

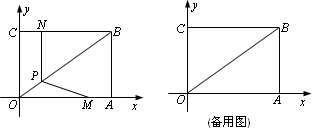
(1)点B的坐标为________；用含t的式子表示点P的坐标为________；

(2)记△·MP的面积为S，求S与t的函数关系式(0＜t＜6)；并求t为何值时，S有最大值？

(3)试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△·NC分割成三角形和四边形两部分，且三角形的面积是△·NC面积的？若存在，求出点T的坐标；若不存在，请说明理由．

问题：已知△ABC中，Ð BAC＝2Ð ACB，点D是△ABC内的一点，且AD＝CD，BD＝BA．探究Ð DBC与Ð ABC度数的比值．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．

(1)当Ð BAC＝90°时，依问题中的条件补全下图．观察图形，AB与AC的数量关系为________；当推出Ð DAC＝15°时，可进一步推出Ð DBC的度数为________；

可得到Ð DBC与Ð ABC度数的比值为_________；

(2)当Ð BAC≠90°时，请你画出图形，研究Ð DBC与Ð ABC度数的比值是否与(1)中的结论相同，写出你的猜想并加以证明．

小贝遇到一个有趣的问题：在矩形ABCD中，AD＝8 cm，AB＝6 cm．现有一动点P按下列方式在矩形内运动：它从A点出发，沿着AB边夹角为45°的方向作直线运动，每次碰到矩形的一边，就会改变运动方向，沿着与这条边夹角为45°的方向作直线运动，并且它一直按照这种方式不停地运动，即当P点碰到BC边，沿着BC边夹角为45°的方向作直线运动，当P点碰到CD边，再沿着与CD边夹角为45°的方向作直线运动，…，如图1所示，问P点第一次与D点重合前与边相碰几次，P点第一次与D点重合时所经过的路径的总长是多少．小贝的思考是这样开始的：如图2，将矩形ABCD沿直线CD折迭，得到矩形A₁B₁CD，由轴对称的知识，发现P₂P₃＝P₂E，P₁A＝P₁E．请你参考小贝的思路解决下列问题：

(1)P点第一次与D点重合前与边相碰________次；P点从A点出发到第一次与D点重合时所经过的路径的总长是________cm；

(2)近一步探究：改变矩形ABCD中AD、AB的长，且满足AD＞AB，动点P从A点出发，按照阅读材料中动点的运动方式，并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上．若P点第一次与B点重合前与边相碰7次，则AB：AD的值为________．

设正n边形A₀A₁A₂…A_n－1与正n边形A₀B₁B₂…B_n－1重合(其中A₁与B₁重合)，现将正n边形A₀B₁B₂…B_n－1绕顶点A₀逆时针旋转α(0°＜α)．

(3)设_n与上述“₃，₄，…”的意义一样，请直接写出_n的度数；

(4)试猜想在正n边形的情况下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请将这条线段用相应的顶点字母表示出来(不要求证明)；若不存在，请说明理由．

课题：两个重叠的正多边形，其中的一个绕某一个顶点旋转所形成的有关问题．

设旋转角∠A₁A₀B₁＝α(α＜∠A₁A₀A₂)，₃，₄，₅，₆所表示的角如图所示．

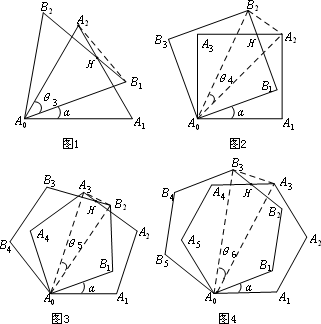
(1)用含α的式子表示角的度数：₃＝________，₄＝________，₅＝________；

(2)图4中，连接A₀H时，在不添加其他辅助线的情况下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请选择其中一个图给出证明；若不存在，请说明理由；

如图，已知抛物线y＝x²＋bx＋c与y轴相交于C，与x轴相交于A、B，点A的坐标为(2，0)，点C的坐标为(0，－1)

(1)求抛物线的解析式；

(2)点E是线段AC上一动点，过点E作DE⊥x轴于点D，连结DC，当△DCE的面积最大时，求点D的坐标；

(3)在直线BC上是否存在一点P，使△ACP为等腰三角形，若存在，求点P的坐标，若不存在，说明理由．

如图1，已知梯形OABC，抛物线分别过点O(0，0)、A(2，0)、B(6，3)．

(1)直接写出抛物线的对称轴、解析式及顶点M的坐标；

(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移，分别交抛物线于点O₁、A₁、C₁、B₁，得到如图2的梯形O₁A₁B₁C₁．设梯形O₁A₁B₁C₁的面积为S，A₁、B₁的坐标分别为(x₁，y₁)、(x₂，y₂)．用含S的代数式表示x₂－x₁，并求出当S＝36时点A₁的坐标；

(3)在图1中，设点D坐标为(1，3)，动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段DM运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

(1)探究新知：

①如图，已知AD∥BC，AD＝BC，点M，N是直线CD上任意两点．

求证：△ABM与△ABN的面积相等．

②如图，已知AD∥BE，AD＝BE，AB∥CD∥EF，点M是直线CD上任一点，点G是直线EF上任一点．试判断△ABM与△ABG的面积是否相等，并说明理由．

(2)结论应用：

如图③，抛物线y＝ax²＋bx＋c的顶点为C(1，4)，交x轴于点A(3，0)，交y轴于点D．试探究在抛物线y＝ax²＋bx＋c上是否存在除点C以外的点E，使得△ADE与△ACD的面积相等？若存在，请求出此时点E的坐标，若不存在，请说明理由．

﹙友情提示：解答本问题过程中，可以直接使用“探究新知”中的结论．﹚

如图①，将一张矩形纸片对折，然后沿虚线剪切，得到两个(不等边)三角形纸片△ABC，△A₁B₁C₁．

(1)将△ABC，△A₁B₁C₁如图②摆放，使点A₁与B重合，点B₁在AC边的延长线上，连接CC₁交BB₁于点E．求证：∠B₁C₁C＝∠B₁BC．

(2)若将△ABC，△A₁B₁C₁如图③摆放，使点B₁与B重合，点A₁在AC边的延长线上，连接CC₁交A₁B于点F．试判断∠A₁C₁C与∠A₁BC是否相等，并说明理由．

(3)写出问题(2)中与△A₁FC相似的三角形________．

●探究(1)在图1中，已知线段AB，CD，其中点分别为E，F．

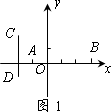
①若A(－1，0)，B(3，0)，则E点坐标为________；

②若C(－2，2)，D(－2，－1)，则F点坐标为________；

(2)在图2中，已知线段AB的端点坐标为A(a，b)，B(c，d)，求出图中AB中点D的坐标(用含a，b，c，d的代数式表示)，并给出求解过程．

●归纳无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A(a，b)，B(c，d)，AB中点为D(x，y)时，x＝________，y＝________．(不必证明)

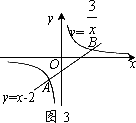
●运用在图2中，一次函数y＝x－2与反比例函数y＝的图象交点为A，B．

①求出交点A，B的坐标；

②若以A，O，B，P为顶点的四边形是平行四边形，

请利用上面的结论求出顶点P的坐标．