如下图，在直角坐标系中，已知点M₀的坐标为(1，0)，将线段OM₀绕原点O沿逆时针方向旋转45°，再将其延长到M₁，使得M₁M₀⊥OM₀，得到线段OM₁；又将线段OM₁绕原点O沿逆时针方向旋转45°，再将其延长到M₂，使得M₂M₁⊥OM₁，得到线段OM₂，如此下去，得到线段OM₃，OM₄，……，OM_n．

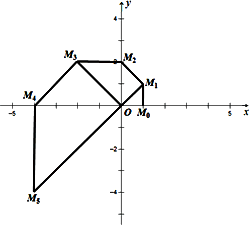
(1)写出点M₅的坐标；

(2)求△M₅OM₆的周长；

(3)我们规定：把点M_n(x_n，y_n)(n＝0，1，2，3……的横坐标x_n，纵坐标y_n都取绝对值后得到的新坐标(|x_n|，|y_n|)称之为点M_n的“绝对坐标”．根据图中点M_n的分布规律，请你猜想点M_n的“绝对坐标”，并写出来．

如图，过点P(－4，3)作x轴、y轴的垂线，分别交x轴、y轴于A、B两点，交双曲线y＝(k≥2)于E、F两点．

(1)点E的坐标是________，点F的坐标是________；(均用含k的式子表示)

(2)判断EF与AB的位置关系，并证明你的结论；

(3)记S＝S_△PEF－S_△OEF，S是否有最小值？若有，求出其最小值；若没有，请说明理由．

如图，把抛物线y＝－x²(虚线部分)向右平移1个单位长度，再向上平移1个单位长度，得到抛物线l₁，抛物线l₂与抛物线l₁关于y轴对称．点A、O、B分别是抛物线l₁、l₂与x轴的交点，D、C分别是抛物线l₁、l₂的顶点，线段CD交y轴于点E．

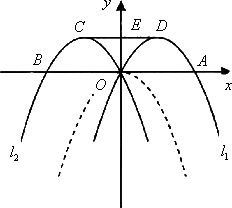
(1)分别写出抛物线l₁与l₂的解析式；

(2)设P是抛物线l₁上与D、O两点不重合的任意一点，Q点是P点关于y轴的对称点，试判断以P、Q、C、D为顶点的四边形是什么特殊的四边形？说明你的理由．

(3)在抛物线l₁上是否存在点M，使得S_△ABM＝S_{△四边形AOED}，如果存在，求出M点的坐标，如果不存在，请说明理由．

如图所示，已知抛物线的图象与y轴相交于点B(0，1)，点C(m，n)在该抛物线图象上，且以BC为直径的⊙M恰好经过顶点A．

(1)求k的值；

(2)求点C的坐标；

(3)若点P的纵坐标为t，且点P在该抛物线的对称轴l上运动，试探索：

①当S₁＜S＜S₂时，求t的取值范围(其中：S为△PAB的面积，S₁为△OAB的面积，S₂为四边形OACB的面积)；

②当t取何值时，点P在⊙M上．(写出t的值即可)

我们容易发现：反比例函数的图象是一个中心对称图形．你可以利用这一结论解决问题．

如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x轴所在的直线绕着原点O逆时针旋转α度角后的图形．若它与反比例函数y＝的图象分别交于第一、三象限的点B、D，已知点A(－m，0)、C(m，0)．

(1)直接判断并填写：不论α取何值，四边形ABCD的形状一定是________；

(2)①当点B为(p，1)时，四边形ABCD是矩形，试求p、α、和m有值；

②观察猜想：对①中的m值，能使四边形ABCD为矩形的点B共有几个？(不必说理)

(3)试探究：四边形ABCD能不能是菱形？若能，直接写出B点的坐标，若不能，说明理由．

如图1，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，点D在边AB上运动，DE平分∠CDB交边BC于点E，CM⊥BD垂足为M，EN⊥CD，垂足为N．

(1)当AD＝CD时，求证：DE∥AC；

(2)探究：AD为何值时，△BME与△CNE相似？

(3)探究：AD为何值时，四边形MEND与△BDE的面积相等？

△ABC中，∠A＝∠B＝30°，AB＝2．把△ABC放在平面直角坐标系中，使AB的中点位于坐标原点O(如图)，△ABC可以绕点O作任意角度的旋转．

(1)当点B在第一象限，纵坐标是时，求点B的横坐标；

(2)如果抛物线y＝ax²＋bx＋c(a≠0)的对称轴经过点C，请你探究：

①当a＝，b＝－，c＝－时，A，B两点是否都在这条抛物线上？并说明理由；

②设b＝－2am，是否存在这样的m的值，使A，B两点不可能同时在这条抛物线上？若存在，直接写出m的值；若不存在，请说明理由．

在平面直角坐标系中，抛物线经过O(0，0)、A(4，0)、B(3，－)三点．

(1)求此抛物线的解析式；

(2)以OA的中点M为圆心，OM长为半径作⊙M，在(1)中的抛物线上是否存在这样的点P，过点P作⊙M的切线l，且l与x轴的夹角为30°，若存在，请求出此时点P的坐标；若不存在，请说明理由(注意：本题中的结果可保留根号)

如图，在锐角三角形ABC中，BC＝12，△ABC的面积为48，D，E分别是边AB，AC上的两个动点(D不与A，B重合)，且保持DE∥BC，以DE为边，在点A的异侧作正方形DEFG．

(1)当正方形DEFG的边GF在BC上时，求正方形DEFG的边长；

(2)设DE＝x，△ABC与正方形DEFG重叠部分的面积为y，试求y关于x的函数关系式，写出x的取值范围，并求出y的最大值．

(1)如图，在正方形ABCD中，M是BC边(不含端点B、C)上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN＝90°，求证：AM＝MN．

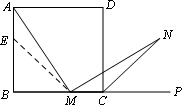
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

证明：在边AB上截取AE＝MC，连ME．正方形ABCD中，∠B＝∠BCD＝90°，AB＝BC．∴∠NMC＝180°－∠AMN－∠AMB＝180°－∠B－∠AMB＝∠MAB＝∠MAE．

(下面请你完成余下的证明过程)

(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图)，N是∠ACP的平分线上一点，则当∠AMN＝60°时，结论AM＝MN是否还成立？请说明理由．

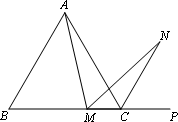
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X”，请你作出猜想：当∠AMN＝________°时，结论AM＝MN仍然成立．(直接写出答案，不需要证明)