科目： 来源： 题型：解答题

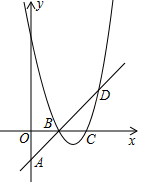16．已知抛物线y=ax²+bx+8（a≥1）过点D（5，3），与x轴交于点B、C（点B、C均在y轴右侧）且BC=2，直线BD交y轴于点A．
（1）求抛物线的解析式；
（2）在坐标轴上是否存在一点N，使△ABN与△BCD相似？若存在，求出点A、N的坐标；若不存在，请说明理由．
（3）在直线BD上是否存在一点P和平面内一点Q，使以Q、P、B、C四点为顶点的四边形为菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

科目： 来源： 题型：解答题

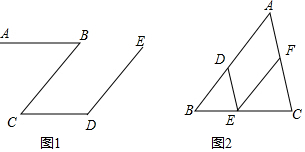15．完成下面的证明（下划线内补全证明过程，括号内填写推理的依据）．
（1）如图1，AB∥CD，∠B+∠D=180°，求证：CB∥DE 
证明：∵AB∥CD（已知）
∴∠B=∠C
∵∠B+∠D=180°（已知）
∴∠C+∠D=180°（等量代换）
∴CB∥DE
（2）如图2，已知DE∥AC，∠A=∠DEF，请证明∠B=∠FEC．
证明：∵DE∥AC（已知）
∴∠A=∠BDE
∵∠A=∠DEF（已知）
∴∠DEF=∠BDE（等量代换）
∴AB∥EF
∴∠B=∠FEC．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

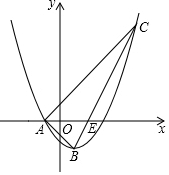13．如图，已知抛物线y=ax²-x+c的对称轴为直线x=1，与x轴的一个交点为A（-1，0），顶点为B．点C（5，m）在抛物线上，直线BC交x轴于点E．
（1）求抛物线的表达式及点E的坐标；
（2）联结AB，求∠B的正切值；
（3）点G为线段AC上一点，过点G作CB的垂线交x轴于点M（位于点E右侧），当△CGM与△ABE相似时，求点M的坐标．

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

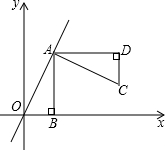11．如图，正比例函数y=kx经过点A（2，4），AB⊥x轴于点B．
（1）求该正比例函数的解析式；
（2）将△ABO绕点A逆时针旋转90°得到△ADC，求点C的坐标；
（3）试判断点C是否在直线y=$\frac{1}{3}$x+1的图象上，说明你的理由．

科目： 来源： 题型：选择题

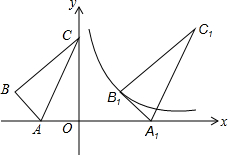10．如图，△ABC的顶点A，C落在坐标轴上，且顶点B的坐标为（-5，2），将△ABC沿x轴向右平移得到△A₁B₁C₁，使得点B₁恰好落在函数y=$\frac{6}{x}$上，若线段AC扫过的面积为48，则点C₁的坐标为（　　）

A．

（3，2）

B．

（5，6）

C．

（8，6）

D．

（6，6）

科目： 来源： 题型：解答题

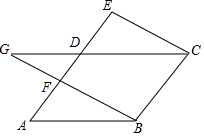9．如图，在?ABCD中，AD=4，AB=5，延长AD到点E，连接EC过点B作BF∥CE交AD于点F，交CD的延长线于点G．
（1）求证：四边形BCEF是平行四边形；
（2）当DF=1时，四边形BCEF是正方形，说明理由；
（3）当$\frac{GF}{GD}$=$\frac{4}{5}$时，四边形BCEF是菱形，说明理由．

科目： 来源： 题型：填空题

8．如图，CD∥AB，且CD=$\frac{1}{2}$AB，点E为AB的中点，若四边形ADCE为正方形，则∠B=45°．

科目： 来源： 题型：选择题