
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:选择题
如果a∶b=3∶2,且b是a,c的比例中项,那么b∶c等于( )
A. 4∶3 B. 3∶2 C. 2∶3 D. 3∶4
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:选择题
如图,有三个直角三角形,其中OA=AB=BC=CD=1,则线段OA,OD的比例中项线段的长度为( )
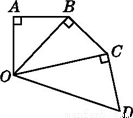
A. 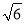 B.
B. 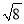 C. ±
C. ±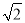 D.
D. 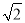
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:选择题
如果点C是线段AB的黄金分割点(AC>BC),则下列比例式正确的是( )
A. AB∶AC=AC∶BC B. AB∶BC=BC∶AC
C. AC∶BC=BC∶AB D. AC∶AB=AB∶BC
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:选择题
若点C为线段AB的黄金分割点,且AC>BC,则
①AB=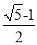 AC;②AC=
AC;②AC=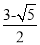 AB;③AB∶AC=AC∶CB;④AC≈0.618AB.其中正确的有( )
AB;③AB∶AC=AC∶CB;④AC≈0.618AB.其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:填空题
从美学角度来说,人的上身长与下身长之比为黄金比时,可以给人一种协调的美感.某女老师上身长约61.80cm,下身长约93.00cm,她要穿约 cm的高跟鞋才能达到黄金比的美感效果(精确到0.01cm)
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:解答题
以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求MA,DM的长;
(2)求证:AM2=AD·DM.
(3)根据(2)的结论你能找出图中的一个黄金分割点吗?
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:解答题
宽与长的比是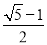 的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):
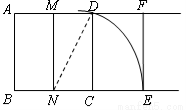
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;
第四步:过E作EF⊥AD,交AD的延长线于F.
请你根据以上作法,证明矩形DCEF为黄金矩形.
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:解答题
如图所示,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(不与顶点重合).如果直线EF将矩形分成面积相等的两部分,那么

(1)得到的两个四边形是否相似?若相似,请求出相似比;若不相似,请说明理由;
(2)这样的直线可以作多少条?
查看答案和解析>>
科目: 来源:人教版数学九年级下册同步练习27.1.2 黄金分割 题型:填空题
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com