
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:单选题
如果一个四边形四个内角度数之比是2∶2∶3∶5,那么这四个内角中( ).
A. 只有一个直角 B. 只有一个锐角 C. 有两个直角 D. 有两个钝角
A 【解析】【解析】 设一份为x,则四个内角分别为:2x,2x,3x,5x,∴2x+2x+3x+5x=360°,解得:x=30°,∴2x=60°,3x=90°,5x=150°,只有一个直角.故选A.查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:单选题
在一个四边形中,如果有两个内角是直角,那么另外两个内角( ).
A. 都是钝角 B. 都是锐角
C. 一个是锐角,一个是直角 D. 互为补角
D 【解析】【解析】 ∵四边形内角和为360°,∴另外两个内角和为180°,互为补角.故选D.查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
从十二边形的一个顶点出发可引_________条对角线,把十二边形分成_______个三角形.
A. 9 10 B. 10 11 C. 11 12 D. 12 13
A 【解析】【解析】 从十二边形的一个顶点出发可引对角线条数:12-3=9,把十二边形分成的三角形个数:9+1=10.故选A.查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
已知:如图四边形ABCD中,∠ABC的平分线BE交CD于E,∠BCD的平分线CF交AB于F,BE、CF相交于O,∠A=124°,∠D=100°.求∠BOF的度数.
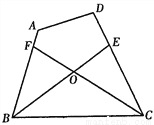
查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
已知:如图,求∠1+∠2+∠3+∠4+∠5+∠6___________.

查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
已知:如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8____________.
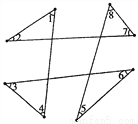
查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
如图,在图(1)中,猜想:∠A+∠B+∠C+∠D+∠E+∠F=______度.
请说明你猜想的理由.
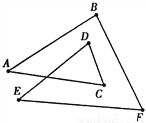
图1
如果把图1成为2环三角形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F;图2称为2环四边形,它的内角和为∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H;
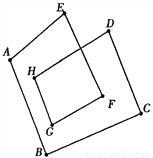
图2
则2环四边形的内角和为_____________________________________________度;
2环五边形的内角和为________________________________________________度;
2环n边形的内角和为________________________________________________度.
(1)360°;(2)720°;(3)1080°;(4)2(n-2)×180° 【解析】【解析】 连结BB1,则∠A1+∠C=∠BB1A1+∠B1BC,∠A+∠B+∠C+∠A1+∠B1+∠C1=∠A+∠ABB1+∠BB1C1+∠C1=360度,得到:2环三角形的内角和为360°; 2环四边形:如图,AA1之间添加两条边,可得B1+∠C1+∠D1=∠EAD+∠AEA1+∠EA1B1 ...查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
一张长方形的桌面,减去一个角后,求剩下的部分的多边形的内角和.
180°或360°或540° 【解析】试题分析:长方形木板据掉一个角以后可能是:三角形或四边形或五边形,根据多边形的内角和定理即可解决. 试题解析:【解析】 长方形木板据掉一个角以后可能是:三角形或四边形或五边形,因而剩下的多边形的内角和是180°或360°或540°.查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
一个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数.
九 【解析】试题分析:根据多边形的内角和公式可知180×7=1260<1350<180×8=1440,所以一个外角只能为1350﹣1260=90,由此得出多边形的边数为7+2=9求得问题. 试题解析:【解析】 设这个多边形的边数为n,180×(n﹣2)=1350﹣,180×7=1260<1350<180×8=1440,所以一个外角只能为1350﹣1260=90,由此得出多边形的边数为...查看答案和解析>>
科目: 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:解答题
如果一个凸多边形除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.
130° 【解析】试题分析:设这个内角为x,根据多边形的内角和公式(n﹣2)•180°可知,多边形的内角度数是180°的倍数,然后利用数的整除性进行求解. 试题解析:【解析】 设这个多边形的边数是n,没有计算在内的内角的度数是x,则(n﹣2)•180°=2570°+x,n=16…50°,180°﹣50°=130°,∴这个多边形是17边形,没有计算在内的内角的度数为130°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com