
科目: 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:解答题
(12分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为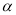 .
.
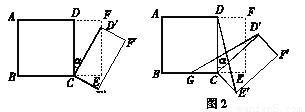
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
(1)30;(2)证明见试题解析;(3)能.或. 【解析】 试题分析:(1)根据旋转的性质得到CD′的长,在Rt△CED′中,CD′=2,CE=1,得到∠CD′E=30°,然后根据平行线的性质即可得到∠α的度数; (2)由G为BC中点可得CG=CE,再根据旋转的性质得∠D′CE′=∠DCE=90°,CE=CE′=CG,则∠GCD′=∠DCE′=90°+α,再根据“SAS”可判断△...查看答案和解析>>
科目: 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:解答题
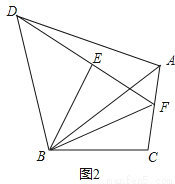
将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF.
(1)如图1,若∠ABC=α=60°,BF=AF.
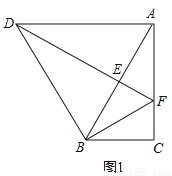
①求证:DA∥BC;②猜想线段DF、AF的数量关系,并证明你的猜想;
(2)如图2,若∠ABC<α,BF=mAF(m为常数),求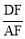 的值(用含m、α的式子表示).
的值(用含m、α的式子表示).
查看答案和解析>>
科目: 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:解答题
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
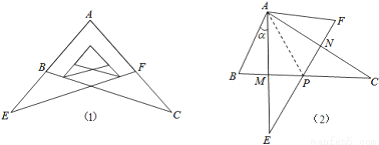
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
(1)证明见解析;(2)当旋转角α=30°时,四边形ABPF是菱形.理由见解析. 【解析】 试题分析:(1)根据旋转的性质得出AB=AF,∠BAM=∠FAN,进而得出△ABM≌△AFN得出答案即可; (2)利用旋转的性质得出∠FAB=120°,∠FPC=∠B=60°,即可得出四边形ABPF是平行四边形,再利用菱形的判定得出答案. 试题解析:(1)∵用两块完全相同的且含60°...查看答案和解析>>
科目: 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:解答题
如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.
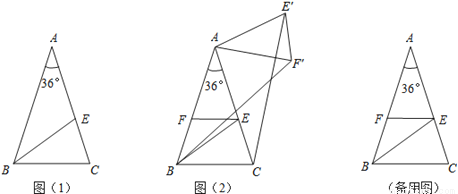
(1)求证:AE=BC;
(2)如图(2),过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到△AE′F′,连结CE′,BF′,求证:CE′=BF′;
(3)在(2)的旋转过程中是否存在CE′∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
【解析】 (1)证明:∵AB=BC,∠A=36°,∴∠ABC=∠C=72°。 又∵BE平分∠ABC,∴∠ABE=∠CBE=36°。 ∴∠BEC=180°﹣∠C﹣∠CBE=72°。∴∠ABE=∠A,∠BEC=∠C。 ∴AE=BE,BE=BC。∴AE=BC。 (2)证明:∵AC=AB且EF∥BC,∴AE=AF; 由旋转的性质可知:∠E′AC=∠F′AB,AE′=AF′,...查看答案和解析>>
科目: 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
在实数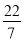 ,-
,-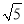 ,
, 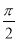 ,
, 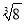 ,3.14 中,无理数有( )
,3.14 中,无理数有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
B 【解析】试题分析:根据无理数是无限不循环小数,可得-, 是无理数. 故选:B查看答案和解析>>
科目: 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
已知一个正方形的边长为a,面积为S,则( )
A. S =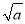 B. S的平方根是a
B. S的平方根是a
C. a是S的算术平方根 D. a=±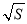
查看答案和解析>>
科目: 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
若点P(x,5)在第二象限内,则x应是( )
A. 正数 B. 负数 C. 非负数 D. 有理数
B 【解析】在第二象限时,横坐标<0,纵坐标>0,因而就可得到x<0,即可得解. 【解析】 ∵点P(x,5)在第二象限, ∴x<0,即x为负数. 故选B. “点睛”解决本题解决的关键是熟记在各象限内点的坐标的符号,第一象限点的坐标符号为(+,+),第二象限点的坐标符号为(-,+),第三象限点的坐标符号为(-,-),第四象限点的坐标符号为(+,-).查看答案和解析>>
科目: 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列函数中,是一次函数的有( )
(1)y=πx;(2)y=2x﹣1;(3)y= ;(4)y=2﹣3x;(5)y=x2﹣1.
;(4)y=2﹣3x;(5)y=x2﹣1.
A. 4个 B. 3个 C. 2个 D. 1个
C 【解析】y=πx属于正比例函数,是特殊的一次函数,属于一次函数;y=2x?1,y=2?3x符合一次函数的定义,属于一次函数,y=属于反比例函数,y=x2﹣1属于二次函数.综上所述,一次函数的个数是3个。故选:B.查看答案和解析>>
科目: 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
点A的位置如图所示,则关于点A的位置下列说法中正确的是( )
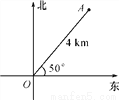
A. 距点O 4 km处 B. 北偏东40°方向上4 km处
C. 在点O北偏东50°方向上4 km处 D. 在点O北偏东40°方向上4 km处
D 【解析】根据方位角的概念可得点A位于O点北偏东40°方向上4km处,故选D.查看答案和解析>>
科目: 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
在平面直角坐标系中,点P(-1,5)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
B 【解析】点P(-1,5)的横坐标为负,纵坐标为正,所以点P在第二象限. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com