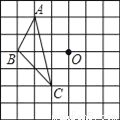
如图，在方格纸中，每个小方格都是边长为1cm的正方形，△ABC的三个顶点都在格点上，将△ABC绕点O逆时针旋转90°后得到△A′B′C′（其中A、B、C的对应点分别为A′，B′，C′，则点B在旋转过程中所经过的路线的长是______cm．（结果保留π）

π 【解析】如下图，由题意可知点B旋转过程中所经过的路线是，∠AOB′=90°，OB=3， ∴=（cm）.

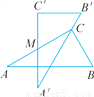
如图是两块完全一样的含30°角的直角三角尺，分别记做△ABC与△A′B′C′，现将两块三角尺重叠在一起，设较长直角边的中点为M，绕中点M转动上面的三角尺ABC，使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上．当∠A＝30°，AC＝10时，两直角顶点C，C′间的距离是_____．

5 【解析】试题分析：连接CC1，根据M是AC、A1C1的中点，AC=A1C1，得出CM=A1M=C1M=AC=5，再根据∠A1=∠A1CM=30°，得出∠CMC1=60°，△MCC1为等边三角形，从而证出CC1=CM，即可得出答案． 【解析】 如图，连接CC1， ∵两块三角板重叠在一起，较长直角边的中点为M， ∴M是AC、A1C1的中点，AC=A1C1， ∴CM=...

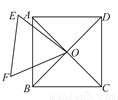
如图，正方形ABCD的对角线相交于点O，正三角形OEF绕点O旋转．在旋转过程中，当AE=BF时，∠AOE的大小是__________．

15°或165° 【解析】分情况讨论：（1）如图（1），连接AE、BF．∵四边形ABCD为正方形，∴OA＝OB，∠AOB＝90°． ∵△OEF为等边三角形，∴OE＝OF，∠EOF＝60°． ∵在△OAE和△OBF中，∴△OAE≌△OBF（SSS）， ∴． （2）如图（2），连接AE、BF．∵在△AOE和△BOF中， ∴△AOE≌△BOF（SSS），∴∠AOE＝∠...

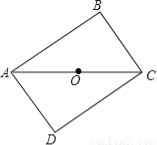
如图所示，将△ABC绕AC的中点O顺时针旋转180°得到△CDA，添加一个条件

　 　，使四边形ABCD为矩形．

∠B=90°。 【解析】∵△ABC绕AC的中点O顺时针旋转180°得到△CDA，∴AB=CD，∠BAC=∠DCA。∴AB∥CD。 ∴四边形ABCD为平行四边形。 当∠B=90°时，平行四边形ABCD为矩形，∴添加的条件为∠B=90°。

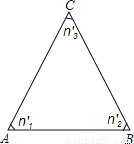
如图，将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3所得到的三角形和△ABC的对称关系是　 　．

关于旋转点成中心对称 【解析】 试题分析：∵n′1+n′2+n′3=180°， ∴将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3，就是将△ABC绕其中一个顶点顺时针旋转180°。 ∴所得到的三角形和△ABC关于这个点成中心对称。

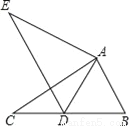
如图，在△ABC中，AB=2，BC=3.6，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为______．

1.6 【解析】试题分析：因为将△ABC绕点A按顺时针旋转一定角度得到△ADE,所以AB="AD=2," 又∠B=600,所以△ABD是等边三角形，所以BD=2，因为BC=3．6,所以CD=BC-BD=3．6-2=1．6．

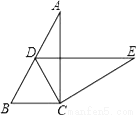
如图，在Rt△ABC中，∠ACB=90°，∠A=α，将△ABC绕点C按顺时针方向旋转后得到△EDC，此时点D在AB边上，则旋转角的大小为______．

2a 【解析】试题分析：：∵在Rt△ABC中，∠ACB=90°，∠A=α，∴∠B=90°-α，由旋转的性质可得：CB=CD， ∴∠CDB=∠B=90°-α，∴∠BCD=180°-∠B-∠CDB=2α．即旋转角的大小为2α．

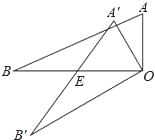
如图，△AOB中，∠AOB=90°，AO=3，BO=6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为 ．

. 【解析】试题分析：利用勾股定理列式求出AB=，根据旋转的性质可得AO=A′O=3，A′B′=AB=，再求出OE=BO=3，从而得到OE=A′O，过点O作OF⊥A′B′于F，利用△A′OB′的面积求出OF=，在Rt△EOF中，利用勾股定理列式求出EF=，再根据等腰三角形三线合一的性质可得A′E=2EF=，然后根据B′E=A′B′﹣A′E=-=． 故答案为：.

如图所示，正方形ABCD中，E是CD上一点，F在CB的延长线上，且DE=BF．

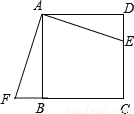
（1）求证：△ADE≌△ABF；

（2）问：将△ADE顺时针旋转多少度后与△ABF重合，旋转中心是什么？

【解析】 （1）证明：在正方形ABCD中，∠D=∠ABC=90°，∴∠ABF=90°。 ∴∠D=∠ABF=90°。 又∵DE=BF，AD=AB， ∴△ADE≌△ABF（SAS）。 （2）将△ADE顺时针旋转90后与△ABF重合，旋转中心是点A。 【解析】 试题分析：（1）根据SAS定理，即可证明两三角形全等。 （2）将△ADE顺时针旋转后与△ABF重合，...

四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF。

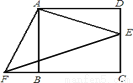
（1）求证：△ADE≌△ABF；

（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；

（3）若BC=8，DE=6，求△AEF的面积。

（1）证明见解析；（2）A，90；（3）50. 【解析】试题分析：（1）根据正方形的性质得AD=AB，∠D=∠ABC=90°，然后利用“SAS”易证得△ADE≌△ABF； （2）由于△ADE≌△ABF得∠BAF=∠DAE，则∠BAF+∠BAE=90°，即∠FAE=90°，根据旋转的定义可得到△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90 度得到； （3）先利用勾股定...