练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

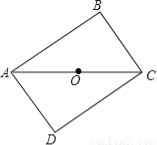
    如图所示，将△ABC绕AC的中点O顺时针旋转180°得到△CDA，添加一个条件

    　 　，使四边形ABCD为矩形．

    ∠B=90°。 【解析】∵△ABC绕AC的中点O顺时针旋转180°得到△CDA，∴AB=CD，∠BAC=∠DCA。∴AB∥CD。 ∴四边形ABCD为平行四边形。 当∠B=90°时，平行四边形ABCD为矩形，∴添加的条件为∠B=90°。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：填空题

    抛物线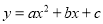 (a>0)的对称轴为直线x=1,且经过点（—1，y1），（2，y2）则试比较y1与y2的大小：y1__________y2（填“>”“<”或“=”）。

    > 【解析】∵二次函数y=ax2+bx+c的图象的对称轴为直线x=1， 而1-（-1）=2，2-1=1， ∴点（-1，y1）离对称轴的距离比点（2，y2）要远， ∴y1＞y2． 故答案为＞．

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    已知一次函数的图象过M（1，3），N（-2，12）两点．

    （1）求函数的解析式；

    (2)试判断点P（-2，-6）是否在函数的图象上，并说明理由．

    (1) y=-3x+6;(2)见解析. 【解析】试题分析： (1)用待定系数法求一次函数的解析式； (2)把x=-2代入到一次函数的解析式中，看函数值是否等于-6. 试题解析： (1)设一次函数的解析式为 y=kx+b， ，解得 所以y=-3x+6 (2)∵当 x=-2 时，y=12≠-6，∴P不在直线上.

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    已知一个正方形的边长为a，面积为S，则（ ）

    A. S =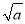 B. S的平方根是a

    C. a是S的算术平方根 D. a=±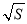

    C 【解析】因为S=a2，所以： A.错误； B.S的算术平方根是a，所以B错误； C.a是S的算术平方根，正确； D.因为a＞0，所以a=，所以D错误. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（1）测试 题型：解答题

    如图所示，正方形ABCD中，E是CD上一点，F在CB的延长线上，且DE=BF．

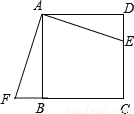
    （1）求证：△ADE≌△ABF；

    （2）问：将△ADE顺时针旋转多少度后与△ABF重合，旋转中心是什么？

    【解析】 （1）证明：在正方形ABCD中，∠D=∠ABC=90°，∴∠ABF=90°。 ∴∠D=∠ABF=90°。 又∵DE=BF，AD=AB， ∴△ADE≌△ABF（SAS）。 （2）将△ADE顺时针旋转90后与△ABF重合，旋转中心是点A。 【解析】 试题分析：（1）根据SAS定理，即可证明两三角形全等。 （2）将△ADE顺时针旋转后与△ABF重合，...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（1）测试 题型：填空题

    如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB=______°．

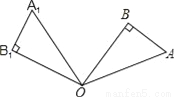
    70 【解析】试题分析：根据旋转的性质可知，∠A1OA=100°，因为∠AOB=30°，所以∠A1OB=100°-30°=70°． 故答案为：70．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册数学第13章13.3《等腰三角形》 题型：填空题

    等腰三角形的周长为13cm，其中一边长为5cm，则该等腰三角形的腰边长为_____cm.。

    5或4 【解析】当5cm是等腰三角形的底边时，则其腰长是（13-5）÷2=4（cm），能够组成三角形； 当5cm是等腰三角形的腰时，则其底边是13-5×2=3（cm），能够组成三角形． 故答案为：5或3.

    查看答案和解析>>

    科目：初中数学 来源：贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型：解答题

    如图，在等边△ABC中，边长为6，D是BC边上的动点，∠EDF=60°．

    （1）求证：△BDE∽△CFD；

    （2）当BD=1，CF=3时，求BE的长．

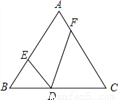
    【答案】（1）证明见解析；(2)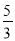

    【解析】试题分析：

    （1）由题意可得，∠B=∠C=60°，∠BDE+∠CDF=120°，∠BDE+∠BED=120°，由此可得：∠CDF=∠BED，从而可得：△BDE∽△CFD；

    （2）由△BDE∽△CFD可得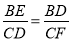： ，由已知易得：CD=BC-BD=5-1=4，由此可得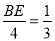： ，解得BE=.

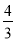    试题解析：

    （1）∵△ABC是等边三角形，

    ∴∠B=∠C=60°，

    ∴∠BDE+∠BED=120°.

    ∵∠EDF=60°，

    ∴∠BDE+∠CDF=120°，

    ∴∠CDF=∠BED，

    ∴△BDE∽△CFD；

    （2）∵等边△ABC的边长为5，BD=1，

    ∴CD=BC-BD=4.

    ∵△BDE∽△CFD，

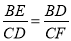    ∴，即，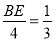

    ∴BE=.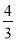

    点睛：本题解题的关键是：由∠EDF=∠B=60°，得到∠BDE+∠BED=120°和∠BDE+∠CDF=120°，从而得到∠BED=∠CDF.

    【题型】解答题
    【结束】
    25

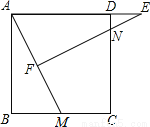
    如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．

    （1）求证：△ABM ∽△EFA；

    （2）若AB=12，BM=5，求DE的长．

    （1）证明见解析；（2）4.9. 【解析】试题分析：（1）由正方形的性质得出AB=AD，∠B=90°，AD∥BC，得出∠AMB=∠EAF，再由∠B=∠AFE，即可得出结论； （2）由勾股定理求出AM，得出AF，由△ABM∽△EFA得出比例式，求出AE，即可得出DE的长． 试题解析：（1）∵四边形ABCD是正方形， ∴AB=AD，∠B=90°，AD∥BC， ∴∠AMB=...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第25章小结与复习 测试 题型：填空题

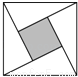
    “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．小亮随机地向大正方形内部区域投飞镖．若直角三角形两条直角边的长分别是 2和1，则飞镖投到小正方形（阴影）区域的概率是 .

    【解析】由题意可得大正方形的面积为：22+12=5，小正方形的面积为12=1，所以 P（飞镖投到小正方形（阴影）区域）= .

    查看答案和解析>>

    同步练习册答案