
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:填空题
从正方形的铁皮上,截去2cm宽的一条长方形,余下的面积是48cm2,则原来的正方形铁皮的面积是 .
64cm2 【解析】 试题分析:设正方形的边长为,截去2cm宽的一条长方形后,还余下一个长方形,长方形的长为,宽为,面积,解得所以原来正方形铁皮的面积为查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:填空题
小亮同学想在房子附近开辟一块绿化场,现共有a米长的篱笆材料,他设计了两种方案:一种是围成正方形的场地,另一种是围成圆形的场地,那么选用哪一种方案围成的场地面积较大________(填序号).
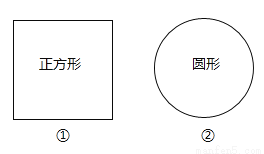
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:填空题
若一梯形的上底长是下底长的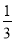 ,高为上底上的4倍还多1,如果下底为x,则梯形的面积S与下底x的函数关系式为________.
,高为上底上的4倍还多1,如果下底为x,则梯形的面积S与下底x的函数关系式为________.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:填空题
某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料的总长为15m,若AB=xm,BC=ym,则y与x的函数解析式为______,窗户的面积S与x的函数解析式为_____,当x≈______时,S最大≈_____,此时通过的光线最多(结果精确到0.01m)
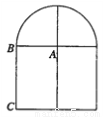
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
已知△ABC中,BC=8,BC上高h=4,D为BC上一点,EF∥BC,交AB于点E,交AC于点F(E、F不过A、B),设E到BC的距离为x,则△DEF的面积y关于x的函数图象大致为(如图所示)()
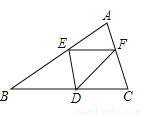
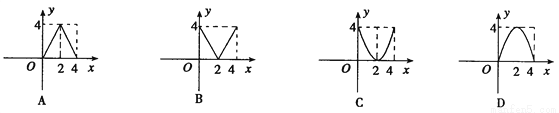
A. A B. B C. C D. D
D 【解析】过点A向BC作AH⊥BC于点H,所以根据相似比可知: , 即EF=,所以,故选D.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
用长8m的铝合金制成如图所示形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是()

A. 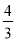 m2 B.
m2 B. 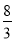 m2 C. 4m2 D.
m2 C. 4m2 D. 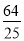 m2
m2
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
在一个近似直角三角形的空地上要挖一长方形的水池,要求长方形水池的两个边在直角三角形空地的直角边上,若测量出直角三角形的三边长分别为30m,40m,50m,则水池的最大面积可以为()
A. 300m2 B. 325m2 C. 400m2 D. 285m2
A 【解析】如图所示, 设DF=x,DE=y,在△ABC中,DF∥AB,可得,即, 同理可得,即, 由AD+CD=AC,可得: ,则矩形花园的面积, 当且仅当x=15,y=20时, ,则AD=CD=25,即点D为AC的中点时,矩形花园的面积最大,且为300,故选A.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:解答题
一养鸡专业户计划用116m长的篱笆围成如图所示的三间长方形鸡舍,门MN宽2m,门PQ和RS的宽都是1m,怎样设计才能使围成的鸡舍面积最大?
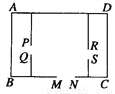
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:解答题
如图,在矩形ABCD中,AB=6m,BC=12m,点P从点A出发沿AB边向B以1m/s的速度运动,同时点Q从点B出发,沿BC边向点C以2m/s的速度运动,P、Q两点在分别到达B、C两点后就停止运动,设经过ts时,△PBQ的面积为Sm2,则
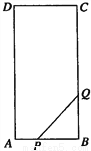
(1)S与t的函数解析式为:S=_________;
(2)用表格表示:
t/s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
S/m2 |
(3)用图象表示:
(4)在这个问题中,自变量t的取值范围是______;图象的对称轴是_______,顶点坐标是________;当t<______时,S的值随t值的增大而_______;当t>______时,S的值随t值的增大而_______(填“增大”或“减小”);当t=______时,S取得最大值为_______.
(1)-t2+6(2)填表见解析(3)图像见解析(4)0≤t≤6;t=3;(3,9);3;增大;3;减小;3;9 【解析】试题分析:(1)根据t秒时,P,Q两点的运动路程,分别表示PB,BQ的长度,可得△BPQ的面积S, (2)把t的值代入解析式可求得对应的S, (3)通过表格,描点,连线即可求解, (4)根据二次函数的图象性质可求解. 试题解析:(1)第t秒时,AP...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:解答题
如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同,正常水位时,大孔水面宽度AB=20m,顶点M距水面6m(即MO=6m),小孔顶点N距水面4.5m(即NC=4.5m),当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
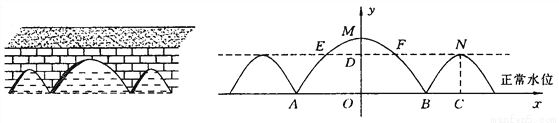
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com