
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
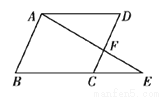
如图所示,已知平行四边形ABCD,E是BC延长线上的一点,连接AE交CD于点F,若AB=3,AF=4,DF=2时,求AE的长.
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
将油箱注满 k 升油后,轿车行驶的总路程S(单位:千米)与平均耗油量 a(单位:升 / 千米)之间是反比例函数关系 S = 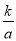 (k 是常数,k≠0).已知某轿车油箱注满油后,以每千米平均耗油 0.1 升的速度行驶,可行驶 500 千米.
(k 是常数,k≠0).已知某轿车油箱注满油后,以每千米平均耗油 0.1 升的速度行驶,可行驶 500 千米.
(1)求该轿车可行驶的总路程 S 与平均耗油量 a 之间的函数解析式(关系式);
(2)当平均耗油量为 0.08 升 / 千米时,该轿车可以行驶多少千米?
(1)s=;(2)625千米 【解析】(1)把a=0.1,S=700代入得: ,解得k=70,∴. (2)把a=0.08代入得:S=875. 故该矫车可以行驶875千米.查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点P.
(1)以A点为位似中心,将△ABC在网格中放大成△AB1C1,使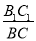 =2,请画出△AB1C1;
=2,请画出△AB1C1;
(2)以P点为三角形的一个顶点,请画一个格点△PMN,使△PMN∽△ABC,且相似比为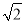 .
.
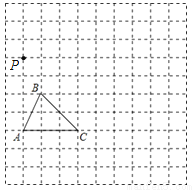
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
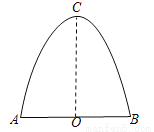
有一辆载有长方体形状集装箱的货车想通横截面为抛物线的隧道,如图所示,已知隧道底部宽AB为 4 m,高OC为 3.2 m,集装箱的宽与货车的宽都是 2.4 m,集装箱顶部离地面 2.1 m.这辆货车能通过这个隧道吗?请说明理由.
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
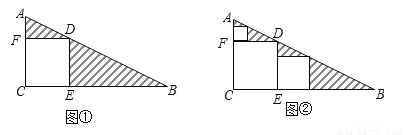
三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求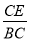 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
如图,一次函数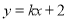 的图象与反比例函数
的图象与反比例函数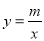 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交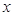 轴、
轴、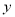 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, 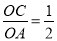 .
.
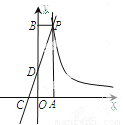
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当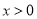 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的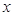 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
某商场销售同型号A、B两种品牌节能灯管,它们进价相同,A品牌售价可变,最低售价不能低于进价,最高利润不超过4元,B品牌售价不变.它们的每只销售利润与每周销售量如下表:(售价=进价+利润)

(1)当A品牌每周销售量为300只时,B品牌每周销售多少只?
(2)A品牌节能灯管每只利润定为多少元时?可获得最大总利润,并求最大总利润.
(1)500;(2)A品牌灯管每只利润为2.4元时,可获得最大总利润,每周最大利润为2008元. 【解析】【试题分析】 (1)根据A品牌的销售量表达式 ,得=300,解方程得:x=3,当x=3时,B品牌对应的销售量的表达式 ,即B品牌每周销售量为500只. (2)分类讨论:利润=A的利润+ B的利润,则设每周总利润为y元,则 当0<x≤3时, y= == 当x=2.4...查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
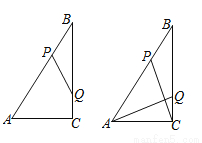
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)当t为何值时,四边形ACQP的面积最小,最小值是多少?
(3)连接AQ,CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目: 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:单选题
将方程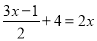 去分母,正确的是( )
去分母,正确的是( )
A. 3x﹣1=﹣4x﹣4 B. 3x﹣1+8=2x C. 3x﹣1+8=0 D. 3x﹣1+8=4x
D 【解析】试题分析:方程两边同乘2得: 3x-1+8=4x, 故选D.查看答案和解析>>
科目: 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:单选题
把方程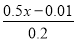 ﹣0.5=
﹣0.5=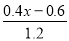 的分母化为整数,正确的是( )
的分母化为整数,正确的是( )
A. 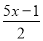 ﹣0.5=
﹣0.5=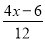 B.
B. 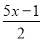 ﹣0.5=
﹣0.5=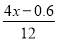
C. 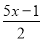 ﹣0.5=
﹣0.5=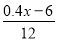 D.
D. 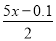 ﹣0.5=
﹣0.5=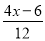
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com