练习册

  • 练习册
  • 试题
    相关习题
     0  319367  319375  319381  319385  319391  319393  319397  319403  319405  319411  319417  319421  319423  319427  319433  319435  319441  319445  319447  319451  319453  319457  319459  319461  319462  319463  319465  319466  319467  319469  319471  319475  319477  319481  319483  319487  319493  319495  319501  319505  319507  319511  319517  319523  319525  319531  319535  319537  319543  319547  319553  319561  366461 

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：单选题

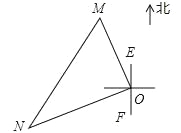
    一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处，若M、N两点相距100海里，则∠NOF的度数为（ ）

    A. 50° B. 60° C. 70° D. 80°

    C 【解析】试题分析：∵OM=60海里，ON=80海里，MN=100海里，∴OM2+ON2=MN2，∴∠MON=90°，∵∠EOM=20°，∴∠NOF=180°﹣20°﹣90°=70°．故选C．

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：单选题

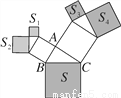
    如图，所有三角形都是直角三角形，所有四边形都是正方形，已知S1＝4，S2＝9，S3＝8，S4＝10，则S＝(　　)

    A. 25 B. 31 C. 32 D. 40

    B 【解析】试题分析：如图，分别求出AB2、AC2，进而得到BC2，即可解决问题． 【解析】 如图，由题意得： AB2=S1+S2=13， AC2=S3+S4=18， ∴BC2=AB2+AC2=31， ∴S=BC2=31， 故选B．

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：单选题

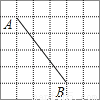
    如图，在边长为1个单位长度的小正方形组成的网格中，点A、B都是格点，则线段AB的长度为（ ）

    A. 5 B. 6 C. 7 D. 25

    A 【解析】试题分析：根据图形，利用勾股定理可得：，故选：A．

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：填空题

    如图，从电线杆离地面3米处向地面拉一条长为5米的拉线，这条拉线在地面的固定点距离电线杆底部有___________米。

    4 【解析】在Rt△ABC中，BC=3，AC=5， 由勾股定理，得AB2=AC2-BC2=52-32=42， 所以AB=4（米）． 所以地面拉线固定点A到电线杆底部的距离为4米． 故答案是：4．

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：填空题

    在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4=_______

    4 【解析】试题分析：根据三角形全等的性质以及勾股定理可得：=1，=3，则+=4.

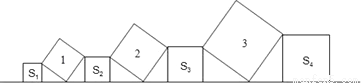
    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：填空题

    学校有一块长方形的花圃如右图所示，有少数的同学为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了________步（假设1米=2步），却踩伤了花草，所谓“花草无辜，踩之何忍”！

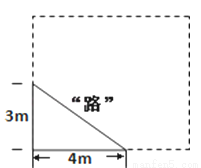
    4 【解析】在Rt△ABC中,AB²=BC²+AC²， 则AB==5m， 少走了2×(3+4?5)=4(步). 故答案为：4.

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：填空题

    在Rt△ABC中，∠C=90°，AB=1，则AB2+BC2+AC2=__．

    2 【解析】由勾股定理得，BC2+AC2=1，则AB2+BC2+AC2=2.

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：填空题

    如图，正方形ABCD中，AE⊥BE于E，且AE=3，BE=4，则阴影部分的面积是_______．

    19 【解析】∵AE=3，BE=4， . .

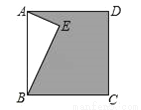
    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：解答题

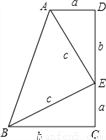
    如图，在梯形ABCD中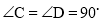， 利用面积法证明勾股定理．

    证明见解析. 【解析】试题分析： 用以下两种方法分别计算梯形ABCD的面积，再利用同一个几何图形的面积相等得到等式变形即可证明得到“勾股定理”； 方法（1）：S梯形= (上底+下底) 高；方法（2）：S梯形=S△ABE+S△ADC+S△BCE； 试题解析： 由题意可得：在△ADE和△ECB中， ， ∴△ADE≌△ECB， ∴∠AED=∠EBC， ∵E...

    查看答案和解析>>

    科目： 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：解答题

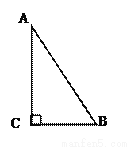
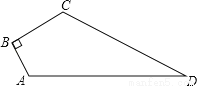
    如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．

    36． 【解析】 试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积． 【解析】 连接AC，如图所示： ∵∠B=90°， ∴△ABC为直角三角形， 又∵AB=3，...

    查看答案和解析>>

    同步练习册答案