
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
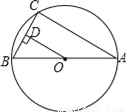
如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为______.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
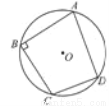
如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是_______
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
在周长为26π的⊙O 中,CD 是⊙O 的一条弦,AB 是⊙O 的切线,且 AB∥CD,若 AB 和CD 之间的距离为18,则弦CD 的长为 .
24 【解析】试题解析:如图,设AB与O相切于点F,连接OF,OD,延长FO交CD于点E. ∵2πR=26π, ∴R=13, ∴OF=OD=13, ∵AB是O切线, ∴OF⊥AB, ∴EF⊥CD即OE⊥CD, ∴CE=ED, ∵EF=18,OF=13, ∴OE=5, 在RT△OED中, ∴CD=2ED=24. 故答案为2...查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是__.
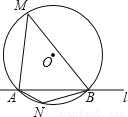
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
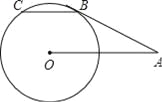
如图,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA,劣弧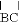 的弧长为 .(结果保留π)
的弧长为 .(结果保留π)
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
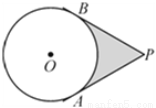
如图,P 为⊙O 外一点,PA、PB 是⊙O 的切线,A、B 为切点,已知PA=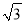 ,∠P=60°,则图中阴影部分的面积为 .
,∠P=60°,则图中阴影部分的面积为 .
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
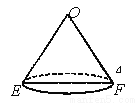
如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10 cm,母线OE(OF)长为10 cm.在母线OF上的点A处有一块爆米花残渣,且FA = 2 cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为_________.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:解答题
“五段彩虹展翅飞”,横跨南渡江的琼州大桥如图,该桥的两边均有五个红色的圆拱,如图(1).最高的圆拱的跨度为110m,拱高为22m,如图(2),那么这个圆拱所在圆的直径为多少米?
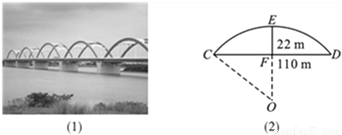
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:解答题
如图,⊙O 是△ABC 的外接圆,AB 为直径,OD∥BC 交⊙O于点D,交AC 于点E,连接AD、BD、CD,求证:AD=CD.
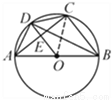
查看答案和解析>>
科目: 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:解答题
如图,已知在⊙O中,AB= 4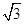 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
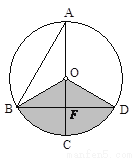
⑴求图中阴影部分的面积;
⑵若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.
(1)阴影部分的面积为;(2)这个圆锥底面圆的半径为. 【解析】试题分析:(1)由∠A=30°,可求得∠BOC=60°,再根据垂径定理得∠BOD=120°,由勾股定理得出BF以及OB的长,从而计算出阴影部分的面积即扇形的面积. (2)直接根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得圆锥的底面圆的半径. 试题解析:(1)∵AC⊥BD于F,∠A=30°, ∴∠BOC=60...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com